Please quote 2pcs sample evaluation and then 25pcs regular order of attached 4” SiC 4H-SiC Thanks Yunling Specification of 4H-SiC wafer- Sr. No. Physical Property Quantitative value Offered Value Compliance Yes/No 1 Material Single Crystal Silicon Carbide (SiC) 2 Polytype 4H-SiC 3 Diameter 100 ±0.5 mm (Without Primary & Secondary flats) 4 Thickness 1 mm ± 50 µm 5 Type n-type 6 Surface Orientation ON axis <0001> ± 0.5o 7 Micropipe density ≤ 2 / cm2 8 FWHM of X-ray Rocking Curve ≤ 25 arc sec 9 TTV ≤ 25 µm full substrate 10 Warp ≤ 50 µm full substrate 11 Surface Carbon face CMP polished, Surface roughness<0.5nm; Silicon face Optical polished. 12 Laser Marking Laser marking on Silicon face.
What is a Rocking Curve?
Rocking Curve Spec Included With Wafer Quotes
A Phd student requested a quote for the following:
I am interested in GaN-on-Si (wafers / templates). Size: 2-inch. n-type doping (if possible), epi-ready.
UniversityWafer, Inc. quoted:
Ø2'' SSP Silicon <111> Wafers with N-type GaN on Silicon,Doping level ~10^18,Epi ready, GaN thickness is 3.5 microns. Silicon 625um thick,Qty. 10
GaN thickness: 3.43um measured by PL
Si doping: <1E18/cc
X-ray rocking curves: 519.8 arcsec @ XRD 002
661.1 arcsec @ XRD 102
Threading dislocation density: Less than 5*109 cm-2
AFM surface roughness: <1nm
Pls see below for the offer on qty. 10
Ø2'' SSP Silicon <111> Wafers with N-type GaN on Silicon,Doping level ~10^18,Epi ready, GaN thickness is 3.5 microns. Silicon 625um thick,Qty. 10pcs
Reference #267167 for pricing
Get Your Quote FAST! Or, Buy Online and start Researching Today1
Silicon Carbide (SiC) Rocking Curve
A seasoned researcher requested a quote for the following:
UniversityWafer, Quoted:
4” SiC 4H-SiC
Specification of 4H-SiC wafer- Sr. No. Physical Property Quantitative value Offered Value Compliance Yes/No
1 Material Single Crystal Silicon Carbide (SiC)
2 Polytype 4H-SiC
3 Diameter 100 ±0.5 mm (Without Primary & Secondary flats)
4 Thickness 1 mm ± 50 µm
5 Type n-type
6 Surface Orientation ON axis <0001> ± 0.5o
7 Micropipe density ≤ 2 / cm2
8 FWHM of X-ray Rocking Curve ≤ 25 arc sec
9 TTV ≤ 25 µm full substrate
10 Warp ≤ 50 µm full substrate
11 Surface Carbon face CMP polished, Surface roughness<0.5nm; Silicon face Optical polished.
12 Laser Marking Laser marking on Silicon face.
13 Quantity: 2 & 25pcs
Reference #267652 for pricing.
Sapphire Wafers Rocking Curve
A university scientist requested a qutoe for the following:
Please quote price and delivery time for 150 nos. sapphire wafers as per detail specs given in PDF document attached. While quoting please confirm you will meet all the specs specified in attached document.
1 inch C-plane (0001) Sapphire Wafers Scope of the Supply: This document specifies the technical requirements for the supply of 1 inch C-plane (0001) Sapphire Wafers, which will be used to deposit thin films. Bid evaluation criteria: 1. The vendor should clearly specify name of the manufacturer of the product along with its part number and provide product literature with the offer. Specifications of the product with part numbers offered must be verifiable from website of the manufacturer. 2. The bidder must mention the actual specifications of their product. “Complied” or “Provided” written against our required specifications will NOT be acceptable under any circumstance. Acceptance Criteria: 1. Cracked or damaged items will not be accepted. 2. Items should be supplied in the proper packing (only in original factory packing). 3. Deviation in dimensions/values of the ordered items will not be accepted. Technical Specifications 1 inch C-plane (0001) Sapphire Wafers, (Qty. 150 nos.) Material: High Purity >99.99%, single crystal Al2O3 Dimension (Diameter): 25.4 mm +/- 0.1 mm Thickness: 600 μm +/- 30 μm or better Lattice Parameter: a=4.785 Å, c=12.991 Å Density: 3.98 g/cm3 Orientation: C plane (<0001> +/-0.5o ) Rocking curve width of : < 180 arcsec (rocking data must be provided) Total Thickness Variation (TTV): <5 μm Bow: <10 μm Warp: <10 μm Thermal Conductivity: 40 W/(m.K) at 20°C Polishing: Double side polished (DSP) Ra < 0.5 nm (AFM image must be provided). Transmittance: > 85% @460 nm (transmission data must be provided) Page 2 of 2 Compliance sheet S. No. Parameters Purchaser’s Values Bidder’s Values 1 inch C-plane (0001) Sapphire Wafers Qty. : 150 nos. 1. Material: High Purity >99.99%, single crystal Al2O3 2. Dimension (Diameter): 25.4 mm +/- 0.1 mm 3. Thickness: 600 μm +/- 30 μm or better 4. Lattice Parameter: a=4.785 Å, c=12.991 Å 5. Density: 3.98 g/cm3 6. Orientation: C plane (<0001> +/-0.5o ) 7. Rocking curve width of : < 180 arcsec (rocking data must be provided) 8. Total Thickness Variation (TTV): <5 μm 9. Bow: <10 μm 10. Warp: <10 μm 11. Thermal Conductivity: 40 W/(m.K) at 20°C 12. Polishing: Double side polished (DSP) Ra < 0.5 nm (AFM image must be provided). 13. Transmittance: > 85% @460 nm (transmission data must be provided)
Reference # 262802 for pricing.
Single Crystal Silicon Rocking Curve
A corporate client requested a quote for the following:
Kindly quote along with HSN code,
1. "Supply of Silicon Si (311) single crystals; Size:100mm X 100mmX10mm" 2 NUMBER
1. General Description
Si (311) Single Crystal (Qty.-2No.)
A pair of Silicon Si (311) crystals for Double crystal monochromator is required at X-ray Photo Emission
Electron Spectroscopy beam line, Indus-2 Synchrotron Radiation facility
2. Scope of Supply
A pair of Silicon Si (311) single crystals for double crystal monochromator for bending magnet
synchrotron beamline applications. The crystals will be used at Indian synchrotron Indus-2 beamline at
bending magnet source.
3. Technical Specifications
Following are technical specifications for Silicon Si (311) crystals.
Crystal Single Crystal Silicon cut to 311 plane
Size: 100mm X 100mmX10mm
Shape plane
Diffraction Rocking curve widths for finished crystals should be within 0.3 arcsec of
the theoretical FWHM of Si (311).
Micro roughness ≤ 3 Å
Slope error ≤3 µrad rms
UHV Compatibility 10-10 mbar
Cryo cooling not needed.
4. Documentation
Metrology test report required for
• Orientation rocking curve measurements.
• Surface finish including slope error and surface roughness.
• Overall shape.
5. Warranty
• One year from the date of acceptance of the system.
Reference #238975 for pricing.
Rocking Curve Explained
A rocking curve is a way to explore a small region of reciprocal space with a constant Q-value. It is the only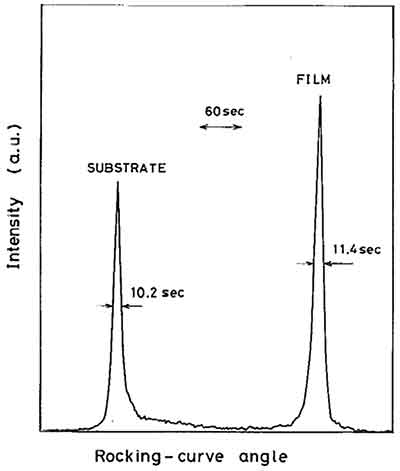 
way to obtain information about the missorientation of different zones. There are two types of rocking curves. One type uses a constant Q-value to explore a small region, and the other uses a variable Q-value.
X-ray rocking curve analysis
X-ray rocking curve analysis is a highly visual task and therefore cannot be encoded in the core of an expert system. It therefore requires a concept formation methodology that elicits key visual features of the domain and uses these as probability indices for referencing solved problems.
In order to create a rocking curve analysis, the observed rocking curves must be normalized. These normalized profiles must contain conventional and HRXRD parameters. A synchrotron is able to produce a delta function for the incident beam, while a diffractometer must be equipped with beam conditioners that control the wavelength distribution.
High-resolution rocking curve analysis can yield valuable information about crystal defect structure. The rocking curve is a specialized method of exploration of a region of reciprocal space that is characterized by a constant Q-value. In this way, it is possible to determine the structure of defects in different zones.
High-resolution X-ray rocking curve analysis is an excellent tool for analyzing epitaxial single crystal films. It enables a better understanding of the composition of the film and its strain state. It also allows for better simulation and analysis of rocking curves in films with a crystalline structure.
The data from rocking curve analysis can help understand the dynamics of heteroepitaxy on an 001 substrate. The rocking curve analysis can also provide insights into the formation of crystalline structure. For example, the formation of heteroepitaxy requires the analysis of the rocking curves of two asymmetric reflections on the same 001 substrate. In addition, the strained alloy layer is assumed to be distorted tetragonally. By using these assumptions, the in-plane and out-of-plane lattice constants can be computed.
The data from rocking curve analysis of ZnSySe12y have been analyzed. The peak separations of ZnSe and GaAs are 780 arc-sec. The ZnSe buffer layer is also observed in this sample. In addition to the asymmetric peak separation, asymmetry between GaAs and ZnSe can also be resolved by recording the rocking curve at opposite azimuths.
X-ray rocking curve analysis is a powerful technique for assessing the dispersion of a sample using diffraction. It is fast and accurate, and provides quantitative information about the dispersion of the sample.
Methods of measuring a rocking curve
The rocking curve is a curve formed by a crystalline system that undergoes a relative deformation. This deformation results from the inverse piezoelectric effect. The width of the rocking curve can be a few hundred arcseconds. Different methods are used for determining the width of the rocking curve.
One method is to calculate the angle of incidence of the incident X-ray (o0) for a point P on the lattice at an azimuth angle ph=0. In this method, the angle of incidence o0 is defined by Bragg's law at the reciprocal lattice point P and the x-rotation angle r.
Another method of measuring a rocking curve involves taking four measurements in succession at 90 degrees intervals. The data obtained by this method can be used to calculate the surface orientation of a wafer. Once this measurement is made, it can be used to find the position of the peak of the rocking curve.
Methods of measuring a rocking curve have their advantages and disadvantages. First, they increase the precision of analysis. The rocking curve can be calculated by using Equations 12 and 15. It is also possible to calculate the surface orientation of a wafer with a small miscut on its surface using the rocking curve obtained from two samples of d0=180deg and Dphph=180deg.
A second method for measuring a rocking curve is to use two-crystal scanners. This method uses different penetration depths of the radiation and allows for the separation of near-surface defects from volume defects. This method uses a special X-ray tube with two-element anode.
The rocking curves of LGS(770 are best defined as a curve that shifts from zero voltage to positive or negative voltage. These curves contain 3000 experimental points. A five-parameter Lorentz function fits these curves well. The position of the curve at zero field is measured before and after each measurement.
The rocking curve is an indicator of the quality of the crystalline lattice. It can be scanned pointwise for fast check, or it can be combined with a mapping tool to produce a quality map. Methods of measuring a rocking curve can help you study the dislocation density, curvature, misorientation, and inhomogeneity of the crystal.
Techniques for analyzing a rocking curve
The rocking curve is a very useful tool for studying imperfections in materials. It enables the study of different types of defects by revealing their structure. For instance, the rocking curve can be used to investigate the degree of dispersion in different zones of a crystal.
Rocking curve analysis involves a special effort to calculate the systematic contributions. The present article emphasizes the main areas that require special analytical treatment and presents typical results for high-quality diamond and silicon crystals. In addition, it provides a comprehensive knowledge of rocking curve scanning. The results can help scientists understand the behavior of these crystals better.
The rocking curve method is one of the main tools in superlattice analysis. It involves measuring the FWHM (full width at half maximum) of the rocking curve peak. It also requires precise measurements in the sample holder and instrument loading. This technique is particularly helpful for analyzing thin films with large defects and high c-axis orientation.
Techniques for analyzing a rocking curvature can also be used to determine the crystal's composition and strain field. Besides evaluating the composition profile and structure, it can also be used to analyze the relaxation of a crystal. It is important to note that the rocking curves are sensitive to defects in the crystal lattice. For this reason, manufacturers try to create crystals with a low number of defects. Silicon carbide is one such crystal.
After performing these measurements, we can compare the results of the two methods. We can first identify the peak width of a sample by observing the different beam positions. In the case of the JD70-101 rocking curve, different beam positions will yield different peaks. The different beam positions give different PERP and PARA orientation topographs. For the rocking curve on the right, the slits cover a part of the sample. However, the left edge shows a less pronounced curvature.
Impact of dispersive effects on rocking curves
The impact of dispersive effects on rocking curve angular misorientation can be quantified by examining images of the subgrain boundary. These images can be observed in the neighbourhood of defects within the bulk crystal. The images of the subgrain boundary can also be used to quantify the glide plane distortion.
The RC of a prismatic sample is often broadened by the presence of one dislocation. This broadening is caused by the crystal lattice distortions caused by viscoplastic deformation. This is the first sign of polygonization. The prismatic RC contains a main peak with FWHM of 0.005deg and two broader peaks in the background.
Modern synchrotron radiation facilities have developed techniques for imaging rocking curves. These techniques use a two-dimensional detector and a CCD camera. The data obtained from these images can be combined with data from several local RCs to reconstruct images. Three-dimensional Bragg diffraction imaging also incorporates RCI with pinhole diffraction topography.
In this study, we used 3D-RCI to follow the deformation of an ice polycrystal. In particular, we studied the plastic deformation within ice grains with 3D-RCI. These images were then used to reconstruct the three-dimensional rocking curves.
Video: Rocking Curve