Hi, I would like to know the orientation details of single crystal Quartz wafer (76.2mm ST-cut 350um DSP Seeded). The orientation is ST cut and my question is how do you define it in terms of miller indices. The crystal structure is hexagonal so may I know the plane and direction of the ST-cut wafer? Apart from the common details, may I know the fracture toughness of all cut single crystal Quartz wafer.
What are Miller Indices?
Researcher Miller Indices Question
A postdoc requested an answer to their Miller Indices question:
UniversityWafer, Replied:
Here, I'd like to attach a detail orientation types list for your reference from which you will see many type orientations. And the the st-cut is 42.75° that the rotation direction is per drawing AT35°15‘.
Reference #225043 for the answer, spec and pricing.
Get Your Quote FAST! Or, Buy Online and Start Researching Today!
What is The Miller Indices of Sapphire Substrates?
A Phd candidate asked the following:
What is the Bravais-Miller indices for M-Axis Sapphire?
Reference #155915 for specs and pricing.
What is The Miller Indices of Silicon Wafers Face?
A graduate student requested the following answer:
I'm interested in purchasing wafer ID: 2066, 662, and 1289. Do these come with a flat, and what orientation is 1289?
Also, if I"m not mistaken I noticed more than these three wafers at the 100micron thickness not too long ago, any eta on when more will be manufactured? What are the miller indices of the flat face? I'm aware the standard is 110, but wanted to confirm before proceeding.
Reference #202042 for specs and pricing.
What is the Miller Indices of Silicon Crystals?
A university student requested an answer to the following:
What plane do you cut the Si wafers at ie what are the Miller indices I would like to purchase 3 cm radius discs of pure Si crystals Let me know the price singles and bulk?
Reference #233951 for your answer.
What is the Miller Indices of Silicon-on-Sapphire (SoS) Wafers?
I'm interested in your SoS wafers for our work on Photonic waveguides. However, I have some questions that I would like to get answered first: What is the resistivity of the Si layer? Is it possible to get Si resistivities in the order of >3000 Ohm.cm? What is the Si crystal orientation in relation to primary flat for the R plane sapphire wafers? What is the purity of the EPI grown Si crystal? What can we expect in terms of monocrystallinity of the Si layer? In addition, I don’t understand how the crystal orientation of cubic silicon can be <0001>, there is one too many miller indices. Also the relative orientation to the primary flat of the wafer isn’t specified.
Reference #262214 for specs and pricing.
Miller Indices Calculator
Enter the values for a, b, and c:
How Miller Indices Can Help Fabricate Photodetectors
A medical equipment engineer requested our help with their project.
In regards to the issue of preferred Miller indices, my studies show that the (111) direction is a suitable option for manufacturing photodetectors due to the better mobility of charge carriers.
If you have any other opinion on this, I would be happy to have it.
Based on what was said, please send the price of the following items for 25 pieces.
-
CdTe
(111), undoped, P-type 10x10x0.9 mm, DSP (25 pcs)
- CdTe (111)B, undoped, P-type 10x10x1.0 mm, SSP with B face to be polished (25 pcs)
Reference #278007 for specs and pricing.
Why Do Researchers Need to Know aSubstrates' Miller Indices?
Miller indices are a way to describe the orientation of crystal planes in a crystal lattice. They are important for researchers in materials science and solid-state physics because they provide a systematic way to describe the surface of a crystal, including its geometry and atomic arrangement.
For example, knowing the Miller indices of a substrate can provide information about the crystal structure of the material, which is critical in determining its properties, such as its mechanical strength, electrical conductivity, and optical properties. This information can then be used to optimize the growth of thin films on the substrate, or to understand how different substrates will interact with the deposited material.
In addition, the Miller indices can be used to calculate the diffraction pattern of a crystal, which is important for characterizing the structure of materials using techniques such as X-ray diffraction or electron diffraction.
Therefore, knowledge of the Miller indices of a substrate is crucial for researchers working in materials science, solid-state physics, and related fields, as it provides valuable information about the structure of the material, which is critical for understanding its properties and for developing new materials and technologies.
Video: What are Miller Indices?
What are Miller Indices?
If you're unfamiliar with the term "miller indices," it's time to review what it means. The Miller indices are symbolic vector representations of atomic planes in a crystal lattice. In mathematics, these numbers are reciprocals of fractional intercepts with crystallographic axes. They represent the orientation of atoms and faces within a crystal lattice.
Unlike the traditional Cartesian coordinate system, Miller indices use a different coordinate system. In the crystallographic system, three perpendicular axes define a plane, while the Cartesian system has five parallel axes. Generally, a plane passes through the origin of a crystal system only if it intersects with the axis of another crystal structure. In other words, if two planes are parallel, their Miller indices will be equal, no matter what direction they are.
In science, the Miller indices are a very simple concept. They refer to the a1, b, and c axes of a cubic crystal. They are also known as Weiss parameters, and are usually written in the same order. They are the reciprocal of zero, so the indices of one crystal are equal to those of the other. This method makes it possible to define an infinite number of planes and surfaces.
While the term is used in many scientific disciplines, Miller indices are more widely used in physical sciences. They are useful for understanding single crystal structures, interpreting X-ray diffraction patterns, and predicting the mechanical properties of a material. Despite the use in science, the fundamental idea behind the Miller indices is that the 'd' of a crystal structure is the same as the number of atoms in its unit cell.
How Are the Miller Indexes Determined For a Crystal Face?
The axial intercepts of a face are inversely proportional to the Miller indices. For example, face DFG has X = 2a, Y = --2b, and Z = 3c. The Miller indices are used to describe crystal faces and crystallographic forms. Here are three examples of crystal faces. To find their Miller indices, first determine the crystallographic form.
Miller-Bravais Indices
The Miller-Bravais indices for crystal faces are values for a specific part of the face. These values are given in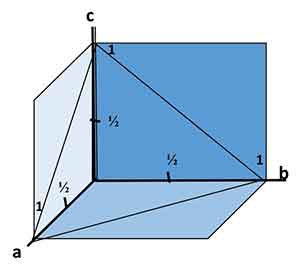
the same order as the Weiss parameters. In the case of triclinic crystals, these values are the a, b, and c axes. For hexagonal and isometric crystals, they are the a1, a2, and a3 axes. Hence, the reciprocal of a number is one.
The Weiss parameters are approximate indications of a face's angular attitude. They act as a symbol for the face and state the number of units at which it intersects each axis. For example, a face with two ao and two bo axes will intercept twice as many ao and bo axes as it cuts the c axis. In contrast, a face with proportions one a: one b: two c = one d.
Another method for assigning a crystal face's symmetry indices is using the Miller-Bravais system. It allows crystal scientists to determine which axes are the same for any given face. The Miller-Bravais indices are usually expressed as angles of 120 degrees. The Miller-Bravais system describes hexagonal crystals and is sometimes referred to as the Bravais-Miller system.
In addition to the Miller-Bravais indices, there are also some special Miller-Bravais indices for hexagonal crystals. Similarity is a characteristic of hexagonal crystals and this is illustrated by the h, k, and l planes of the 4-axis system. These indices are very useful for crystal face analysis. It is possible to determine the symmetry of hexagonal crystal faces by using the Miller-Bravais index system.
If we use the Bravais lattice to solve this problem, then we will need the Miller-Bravais indices. These indices represent the lattice planes of the crystal. Therefore, if you find a plane with zero indices, you will have a crystal with a correspondingly high Miller-Bravais index. A similar analysis is required for non-Bravais lattices.
Miller Indices of Some Planes in Cubic Lattices
When you're making geometrical calculations with a crystal, it's important to remember the Miller indices of some planes in the cubic lattice. These numbers refer to the inverses of the planes' intercepts and define certain aspects of the crystal's structure. If you can't remember them, don't worry, practice problems are available to help you learn the formulas. To practice, simply draw directions on a cubic crystal and find their corresponding points with the same values. Usually, the line from the origin to the points of interest extends infinitely, so you will be able to calculate the Miller indices of some planes in a crystal's face.
The Miller indices of some planes in a cubic lattice are described as positive or negative in a graph. The positive values are those that correspond to the axes in the Cartesian coordinate system, which are front, right, and top. On the other hand, negative values are corresponding to the opposite direction, so we'll see them in Figure 3 as well.
The cubic lattice has six faces, called a hexahedron. The cubic system is unique in that it features extra dimensions: the Miller indices of some planes are a number that describes the symmetry of that crystal. Unlike the lower symmetry crystal systems, the cubic system is unique and has no equivalents in geometry. However, this symmetry is not common in lower-symmetry crystals, and it is important to remember that the Miller indices are not the only properties that make a cubic structure unique.
Some minerals, such as garnet and halite, appear to violate Bravais's Law. In their original study, Bravais' observations had been based on fourteen Bravais lattices and space group symmetries. Later, P. Niggli expanded this idea to screw axes and glide planes, and he and his colleagues concluded that the crystal faces form parallel to the planes with the highest density of atoms.
When you study a single-crystal, a Miller indexed plane will appear with a similar symmetry as the rest of the crystal's faces. The diffraction pattern is reflected on the surface in the same symmetry as the original lattice. The angle of incidence of a beam is proportional to the distance between the beam and the diffraction planes. The direct electron beam will provide a large central spot, but a body-centred cubic lattice will have an equivalent set of Bragg peaks on the halfway position.
Orientation of a Crystal Face
An isometric system is a mathematical representation of a surface's direction in relation to its plane. For example, if the surface's orientation is 90 degrees, it will be 90 degrees if it is a cubic crystal. A cubic crystal is unique. Lower-symmetry crystal systems do not have this symmetry. Orientation is also important to determine the face's plane.
To determine the face's orientation, we must first identify its surface. In crystallography, this surface is called a face. The surface's Miller index is given as one of its smallest integers. This number is then divided by the Miller index to find the face's orientation. The smallest integers, 111, are known as common faces, and 972 are uncommon.
Orientation of a crystal face using a sphere or a cubic cube can be computed by determining the axis and angle of rotation of the crystal. The Miller indices convention defines the orientation of a crystal face. It also provides a way to determine the misorientation between different orientations. The corresponding plot function allows users to visualize the orientation in a sphere or on an axis.
In addition to determining the crystal's symmetry, the orientation of a face is also important to understanding the shape of the unit cell. Some minerals, for example, develop cubic crystals with faces that are nearly identical. But accidents in crystal growth can vary the faces, but the angles between them are rarely significantly off from the ideal. Crystallographers use these angles to determine the symmetry of a crystal face.
The two-dimensional unit cell of hexagonal crystals is a good example of this. The atoms in one unit cell are not aligned with each other. If the crystals have hexagonal symmetry, their unit cells are orthogonal. However, the atoms in a cubic face do not align with one another. If you want to know a crystal's orientation using a miller indices system, you can use a special program to calculate it.
Reciprocals of Weiss Parameters
The equations for Weiss parameters are derived by comparing the intercepts of the face under consideration to those of the unit form. If the face is in unit form, its intercepts will be 2a, 2b, and 2c, respectively. For each axis, the reciprocal of the intercept must be calculated. Then the fractions must be cleared by making a common denominator of one.
In addition to the Weiss parameters, Miller indices can also be calculated to determine a crystal face. Miller indices are derived from the Weiss parameters, but they are not equal to two hundred and ten. In contrast, a crystal face intersecting a crystallographic axis will have a Miller index of a1.
Miller indices are another way to measure the axial intercepts of a crystal face. In crystallography, the two are often called Miller indices. They define the crystal planes and make them quantitatively measurable. Reciprocals of Weiss parameters for a crystal face should allow you to answer questions easily. So what are Miller indices?
The general index (hkl) specifies a face that cuts different axes. Likewise, faces with equal axes are written as h0l, hk0, or la. When calculating Weiss parameters, you must choose a unit face and use that as your reference. You can then use this face to express the intercepts of the other faces.
Miller indices are used to define a family of parallel lattice planes. It is not necessary for these indices to be orthogonal, since they can be orthogonal. The Miller indices are derived from the Weiss zone law and are applicable to any crystal system. If the axes of a crystal face are perpendicular, then the corresponding angle between them will be 90 deg.
Aside from Miller indices, there are also Miller indices, symbolic vector representations for the atomic planes in a crystal lattice. These indices are denoted by parentheses, equivalent faces, or both. A Miller indices ratio of two surfaces illustrates the variations in orientation. This is useful for crystal faces with irregular orientations.
What are Miller Bravais Indices Hexagonal Directions
Hexagonal crystals have four distinct directions. This article will discuss the angle between two given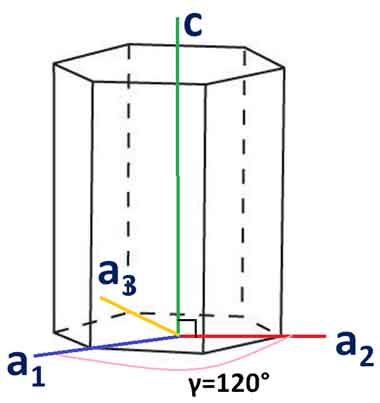 
directions and the Orientation of the plane in hexagonal crystals. It also discusses X-ray diffraction techniques and the Miller-Bravais indices. After reading this article, you should be well-prepared for a lab course or a class in crystallography.
X-ray Diffraction Techniques
X-ray diffraction techniques utilizing miller Bravais indices hexagonal directions are a versatile method of studying crystal structures. The technique relies on a crystal that is crystallized at a specific angle to reflect the X-ray beam. A well-prepared sample should produce a diffraction pattern that resembles a reference sample. Diffraction patterns are highly informative, and often contain impurities that are useful for adjusting chemical reactions. X-ray source and crystallinity of a sample can also affect the diffraction pattern. If crystallization is smaller, the peak will be wider and vice versa.
The three-axis system does not align with hexagonal crystal symmetry. The close-packed directions are not associated with the hexagonal direction because they are not part of the same direction family. Fortunately, there is another approach to determine the hexagonal direction of a crystal. The method uses the Miller-Bravais indices and the concept of side face planes.
The two-axis Miller-Bravais indices are equivalent to one another, and are a convenient way to identify symmetrical crystals. These indices can be converted to normal Miller indices by using a calculator. If you have trouble converting between the two systems, you can use a Miller Index plane calculator from the University of Cambridge.
Another method involves defining the dislocation planes. The dislocation line tends to follow the dense direction. A dislocation plane will be a polygon. The dislocation planes must be defined. It is important to note that Miller indices are integers by definition. However, their physical significance is still not fully understood. Aside from their geometrical basis, they are important for crystallographic studies.
The Miller indices were introduced in 1839 by British mineralogist William Hallowes Miller. They are defined relative to a unit cell, and not primitive basis vectors. These indices are therefore more convenient. For example, when we use them, we can use the Miller indices to estimate the crystallographic orientation of cubic SiC.
Miller-Bravais Indices Determin Lattice Planes
In the world of mathematics, the Miller-Bravais indices determine the family of lattice planes for a given Bravais lattice. They are represented as hkl and bi, which are the basis vectors of a reciprocal lattice. As the name implies, they are proportional to the inverse of the intercept. The three indices h and k are orthogonal, while bi and l are non-orthogonal.
When talking about hexagonal crystals, Miller-Bravais indices are especially useful. They demonstrate that hexagonal crystals have inherent six-fold symmetry. They are also easy to convert, with i = -h+k. If you'd like to convert the indices of hexagonal crystals, you can use a calculator at the University of Cambridge. Listed below are examples of hexagonal crystals and their corresponding Miller-Bravais indices.
Hexagonal direction is the most common type of crystallographic orientation. The Miller-Bravais indices are commonly used to describe hexagonal crystal planes. The a1, a2, and a3 axes of hexagonal unit cells are positive and non-negative. These indices are useful for predicting and comparing hexagonal crystals. However, these indices require careful notation in order to avoid confusion.
The Miller-Bravais indices of hexagonal crystal planes are a useful tool for translating between two axes in the lattice vector normal plane. Whether you're looking for the positive or negative a1 axis, Miller-Bravais indices will help you find the angle that connects two crystal planes. There are also other ways to translate between these two types of planes.
Miller-Bravais Indices Angle between Given Directions
The Miller-Bravais indices are integers that represent the angles between two given crystal structures. For hexagonal crystals, they are used to calculate angles between two given axes in a crystal. To calculate these angles, you must know the direction of each crystal's lattice vector. Once you have a direction, you can calculate the angles by using the corresponding angle functions.
There are several ways to represent the angles between the Miller indices. First, you can group them into families. In the example above, the family 100 consists of the indices (001), (100), and (010). When you use the family, you should always place braces around the indices. The family of planes can also be referred to as a millerian system.
In order to determine the angles between the given miller-Bravais indices, you need to know the direction of each axis. The angle between a given direction and a specific crystal is called its Miller indices. When you have these angles, you can talk about symmetrical crystals. A symmetrical crystal, for example, has slip planes in the close-packed direction.
The Miller indices describe the lattice planes of a crystal in terms of three basis vectors. For hexagonal crystals, an extra axis is added to the equations. These indexes can help you define the angles between different crystal planes and calculate the angle between them. You can find the angle between two given miller indices directions using this formula. There are many ways to calculate this angle.
Orientation of Plane in Hexagonal Crystals
The orientation of a crystal's plane is described by its unit cell, and is often indicated by an equal sign or a Cartesian coordinate system. An example of an orthogonal cell is a hexagonal crystal whose unit cell is oriented with the X and Y axes aligned. This arrangement is known as perfect symmetry. The unit cell of a perfect crystal is oriented in the X and Y axes, but can be rotated by 45 degrees.
The X, Y, and Z axes of a hexagonal crystal are not always perpendicular. In contrast, the X-, Y-, and Z-axes are always perpendicular in cubic and cartesian crystallographic systems. Orientation of plane in hexagonal crystals is therefore not as easy to describe as it is in cubic or cartesian crystals. However, the Miller indices are helpful for describing the orientation of atoms within a crystal.
In cubic crystals, the orientation of the plane can be determined by examining the etch pit figures. The etch pit figures are used to calculate the Miller indices of parallel planes. Alternatively, etch pit figures can be used to determine the orientation of individual crystallites within polycrystalline metals. This method requires the use of an etching reagent. If you want to know more about the etch pit figures, click on the links below.
The plane in a hexagonal crystal is the one which intersects the axes of the structure. It does not intersect the axis, but it crosses it at a distance of one unit. The direction of the plane in hexagonal crystals can be shown with a linear combination of two lattice parameters. A plane is one-quarter the length of the x-axis, so 1/4 across the y-axis is the same.
In addition, when considering the symmetry of hexagonal crystals, it is important to remember that the direction of the plane in a hexagonal system is not necessarily orthogonal. A hexagonal system is not orthogonal if its directions do not match those of the Cartesian coordinates. If you are working with hexagonal crystals, you need to know about the orientation of the plane in hexagonal crystals in order to design atomic systems.
Video: Miller Bravais Indices: Hexagonal Structure
What is Bravais-Miller Indices?
The Bravais-Miller indices are a set of indices used to describe the orientation of crystal planes in a crystal lattice. The indices were first introduced by Auguste Bravais and Charles-Victor Mauguin in the 19th century, and later extended by John D. Miller.
The Bravais-Miller indices are expressed as a set of three integers (h, k, l), which correspond to the number of times that a plane intercepts the unit cell in the crystal lattice along the a, b, and c axes, respectively. The indices are expressed as fractions, and are then reduced to the smallest set of integers that represent the same plane orientation.
For example, if a crystal plane intercepts the unit cell 3 times along the a axis, 4 times along the b axis, and 5 times along the c axis, the Bravais-Miller indices for this plane would be (3, 4, 5).
The Bravais-Miller indices are used to describe the geometry of crystal surfaces, and are important in materials science and solid-state physics for understanding the properties of crystalline materials, such as their electrical conductivity, mechanical strength, and optical properties. They are also used in the analysis of X-ray diffraction patterns, which are a powerful tool for characterizing the structure of crystalline materials.
What are all the Miller Indices Planes
There are an infinite number of possible Miller indices planes, as they describe the orientation of crystal planes in a crystal lattice. The Miller indices of a plane are determined by the ratio of the intercepts of the plane with the unit cell along the crystal lattice's a, b, and c axes.
In general, the Miller indices of a plane can take any positive or negative integer value. Some common examples of Miller indices planes include:
(100), (010), (001), which represent the planes perpendicular to the a, b, and c axes, respectively.
(111), which represents a diagonal plane intersecting the lattice at a 45-degree angle.
(110), (101), (011), which represent planes that intersect the lattice at a 60-degree angle.
(200), (020), (002), which represent planes that intersect the lattice at a 90-degree angle, but are twice as far apart as the (100), (010), and (001) planes.
These are just a few examples of possible Miller indices planes. In general, any set of integers (h, k, l) can represent a Miller indices plane, as long as they describe the ratio of the intercepts of the plane with the unit cell along the a, b, and c axis.