Germanium (Ge) Wafers for Research and Production

university wafer substrates

Germanium Wafers to Fabricate Nanomaterials

A Ph.D. Candidate requested the following quote:

We make nanomaterials in our lab and one approach is using electrical explosion of wires (EEW). We used an old Si wafers (doped with B) and broke off a strip of Si that we attached to electrodes in our EEW apparatus. It worked nicely and we are looking to do the same thing with Ge. We need a wafer that is less than 500 microns thick. Do you have wafers of Ge for sale? We do not need many.

Reference #192550 for specs and pricing.

See our Germanium Wafer Inventory!

Get your Ge Quote FAST! Or, Buy Online and Start Researching Today!

Future of Germanium Substrates

Germanium (Ge) wafers was the first substrate used to make the first transistor. But Ge was expensive compared to Silicon which replaced Ge as the most used material in semiconductor devices. But researchers are working hard to replace silicon with germanium future chips, as it could enable industry to make integrated circuits more efficient, flexible and energy efficient.

 

Czochralski (Cz) Germanium (Ge)

LEDs based on gene and substrates for miniaturization of the chip, but many other implementations are being developed and investigated to explore the future potential of germanium Improved silicon ingot properties based on the present disclosure may include the resulting wafers, resulting solar cells and other applications utilizing the currently disclosed steps for germanium enrichment. Germanium's high-electrical conductivity and low production costs, could help the semiconductor industry to fabricate integrated circuits that have higher power density and lower power consumption than silicon. Ge has proven to be more efficient and cost-effective substrate for producing the next generation of chips and other semiconductor related applications.

The following are just a few of the CZ Ge Wafers available:

CZ Ge
Diameter:200+/-0.1mm
Thickness:2+/-0.1mm
Finish:Double side polished
S/D:60/40

CZ Ge
Diameter:200+/-0.1mm
Thickness:4+/-0.1mm
Finish:Double side polished
S/D:60/40

Cz Ge
Diameter:50+/-0.1mm
Thickness:1+/-0.1mm
Finish:Double side polished
S/D:60/40

Typical Germanium Wafer Packaging

2 inch germanium substrates

Which Keyword have you used to find this page? Tell us and receive a discount on your order!

Germanium wafer prices

  • germanium electrical conductivity
  • germanium wafer singapore
  • germanium wafer thickness
  • germanium wafers manufacturers
  • germanium wafer cost
  • germanium optical material
  • germanium optical properties
  • germanium optical transmission
  • germanium insulator wafer
  • germanium optical window
  • germanium wafer cleaning
  • germanium wafer supplier
  • germanium wafer
  • germanium electrical properties
  • germanium wafers utah
  • germanium optical absorption
  • electrical resistivity pure germanium
  • germanium optical glass
  • germanium-on-insulator substrates by wafer bonding
  • germanium optical grade
  • germanium wafers umicore

What is Germanium Band Gap?

Ge Band Gap is 140 m eV. Let us know if you have any question.

Valence Electrons of Germanium

Valence electrons of Germanium are the four outermost electrons of the element. Its orbital structure is 2-8-18-4, similar to tin and silicon. It is used in technology and industry as a semiconductor material. To understand its properties, you must know about its structure. To determine its valence electrons, you must understand the structure of the elements. Here are some steps to understand its structure:

germanium valence

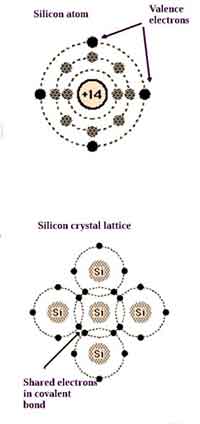
The configuration of electrons in the germanium atom is 1s2 2s2 3p6 d10, with eight valence elements in the last shell. Valence is an important property of elements because it determines their ability to bond. Most other elements do not have constant valence. Instead, it is determined by the formulas of their binary compounds. Listed below are the valence electrons of germanium.

When Germanium was discovered, it was not known what it would be called. The atomic weight of Germanium is around 72. Until 1886, this element had no name. Mendeleev named it ekasilicon, based on a blank space in the periodic table under silicon. He estimated its atomic weight to be somewhere between 70 and 72. Among the elements discovered after that was Germanium.

The second shell has two electrons, the M orbit, and the N orbit. The third orbit and the fourth orbit of the atom are named 'l','m', and 'p'. Each electron has a specific capacity to hold one or more electrons, and it can be up to twenty two electrons in one orbit. Unlike other metals, it is impossible to tell which electrons will be in which shell.

What Is The Total Number Of Valence Electrons In An Atom Of Germanium In The Ground State?

The element germanium has an atomic radius of 125 ppm, and its covalent radius is 122 ppm. Germanium atoms have 32 electrons, with an electron shell structure of [2, 8, 18, 4] with an Atomic term symbol (quantum number) of 3P 0. The electronic configuration at ground state for neutral germanium atoms is [Ar] 3D10 4S2 4P2. The atomic number of germanium (Ge) is 32, Ge is placed in group 14 of periodic table.

Imporant Valence Terms

Below are terms that are associated with Valence Electrons.

  • germanium atoms    
  • metal ions    
  • valence electrons
  • many electrons
  • group atoms
  • charged ions
  • germanium compounds
  • electron
  • different atoms
  • element germanium 
  • nonmetal atoms 
  • atomic number 
  • many germanium
  • outermost electrons 
  • atomic radius    

What is Germanium's Atomic Number?

The atomic number of germanium is 32. The atomic number of an element is the number of protons in the nucleus of an atom of that element. It is a unique identifier for each element and is used to determine the position of an element in the periodic table. The periodic table is a chart that arranges all of the known elements in order of increasing atomic number. Germanium has 32 protons in its nucleus, which places it in the carbon group of the periodic table.

What is Germanium's Band Gap?

Germanium has a band gap of 0.67 eV at room temperature. This means that in order for an electron in germanium to be excited from the valence band (where it is normally found) to the conduction band (where it can conduct electricity), it must be given at least 0.67 eV of energy. This makes germanium a semiconductor, which means it can conduct electricity under some conditions but not others. The band gap of germanium can be adjusted by introducing impurities into the crystal, a process known as doping. This allows germanium to be used in the manufacture of a wide range of electronic devices, such as transistors and solar cells.

In solid-state physics, the band gap is the range of energies in a solid where no electron states can exist. It is the energy difference between the top of the valence band and the bottom of the conduction band in a solid. The band gap of a material has a significant effect on its electrical and optical properties.

Is Germanium a Semiconductor?

Yes, germanium (Ge) is a semiconductor. It is one of the first materials used in semiconductor devices due to its favorable electronic properties. Here's a breakdown of why germanium is classified as a semiconductor:

Key Properties of Germanium as a Semiconductor

  1. Band Gap:

    • Germanium has a relatively small band gap of 0.67 eV at room temperature, compared to silicon's band gap of 1.1 eV. This means that less energy is required to excite electrons from the valence band to the conduction band, making it conductive under certain conditions.

  2. Electrical Conductivity:

    • Germanium’s electrical conductivity lies between that of conductors and insulators, which is characteristic of semiconductors. Its conductivity can be altered by doping with impurities, such as phosphorus or boron.

  3. Intrinsic Carrier Concentration:

    • Due to its small band gap, germanium has a higher intrinsic carrier concentration at room temperature compared to silicon. This makes it more sensitive to temperature changes.

  4. Crystal Structure:

    • Germanium has a diamond cubic crystal structure, similar to silicon, which is conducive for forming covalent bonds and semiconducting behavior.

  5. Applications in Electronics:

    • Germanium was widely used in early transistors and diodes. While silicon has largely replaced it in modern devices due to better thermal stability and availability, germanium is still used in:
      • High-speed electronic devices.
      • Infrared optics.
      • Specialized alloy applications, such as SiGe (silicon-germanium) for high-performance ICs.

  6. Temperature Sensitivity:

    • Germanium's lower thermal conductivity and narrower band gap make it less stable at high temperatures compared to silicon. However, it is more effective at low-voltage and high-frequency operations.

Comparison with Other Materials

  • Advantages over Insulators: Germanium allows some free electron movement, unlike insulators with very large band gaps (e.g., glass or ceramics).
  • Less Popular than Silicon: Silicon is more widely used due to its abundance, better thermal stability, and wider band gap, which minimizes leakage currents.

Conclusion:

Germanium is indeed a semiconductor, playing a foundational role in the development of modern electronics. While its use has decreased with the rise of silicon, it remains relevant in specific high-speed and high-frequency applications.

How Can I Find the Cost of Semiconductor Materials Like Germanium (Ge) Wafers?

The cost of semiconductor materials like germanium depends on the quantity you need to automotive electronics cost as a percentage of total car costspurchase. The price of a small amount is not crucial. The cost of a large quantity is, however, critical. A simple cost comparison shows that silicon is cheaper than germanium. The most important factor in determining the price of a semiconductor is the purity of the material. A high-purity material, such as silicon, will be more expensive than a low-purity one.

When comparing silicon vs. germanium, you will find that silicon is cheaper. This is due to the fact that silicon has a higher melting point than its counterpart. However, you should also take into consideration the lower electrical conductivity of germanium. While this is a consideration, silicon is still more widely used in consumer electronics. For those that are concerned about the price of semiconductor materials, you can compare prices online.

The price of semiconductor materials is an essential element to the cost of electronic devices. As the manufacturing of semiconductors is constantly changing due to new technology, it's important to keep up with the latest prices and research in the industry. In addition, semiconductors are made from many different materials, so it's imperative to stay up-to-date with the latest developments. How can I find the cost of the most common semiconductor materials?

How can I find the cost of semiconductor materials? Today, semiconductor manufacturing has undergone a great change in the way they are made. You can find the latest prices and research by reading industry news. Buying this type of material can be expensive, so you need to know the costs. Fortunately, it's easy to find the price of germanium in the market. So, if you're an electrical engineer, you'll need to know where to buy it and how much it costs.

If you're wondering how to find the cost of semiconductor materials like germanium, you can check out the latest industry news. You can get the latest information about the prices of these materials in the news. You can also read industry-related articles about the current price of the material. These articles are helpful for the research and development of the industry. If you're in the industry of semiconductor manufacturing, you can use the latest material prices in your products.

You can find the cost of semiconductor materials by reading industry news. It's also a good idea to check the price of other materials. Listed below is a list of some of the most popular semiconductor materials. You can find the price of other types of semiconductor materials. Despite the recent price hikes, germanium remains a popular material to purchase. Aside from the competitive advantage, it's inexpensive and easy to obtain.

Various types of semiconductor materials have different properties. For example, silicon is more pure than germanium. It can be used to make computer chips. The disadvantage of using silicon is its low price. It's also a better choice if you need a high-purity semiconductor material. These materials can be used for other electrical purposes and will not have a high price tag. So, check the price before you buy.

In the last two years, silicon has become the preferred choice for manufacturing semiconductor devices. It is cheaper than germanium, and is more easily processed. It also has higher thermal and electrical resistance. Therefore, it is a better choice for consumer electronics. It is not easy to find the cost of semiconductor materials like germanium, but you can check its price on the internet. The best source to buy semiconductor materials is a reputable company that focuses on high quality and reliability.

While the cost of semiconductor materials is important for electronics, it is essential to remember that the price of semiconductor materials can fluctuate dramatically. The best place to buy semiconductor materials is online. If you are a retailer, the pricing of semiconductors is often listed on the website. If you want to purchase a specific type of silicon, you can compare the price against other products that are available. If the cost is higher than you'll pay for a more expensive product, you may want to consider buying less of it.

Germanium (Ge) Substrates

We have a large selection of Electrical and Optical Grade Germanium Single and double side polished wafers in stock and ready to ship.

Buy online and SAVE. If you don't see the spec you need, let us know and we'll quote you!

Germanium wafers for sale

Germanium Wafers for Long-Wave/Mid-Wave Infrared Experiments

Clients have used the following Germanium spec.

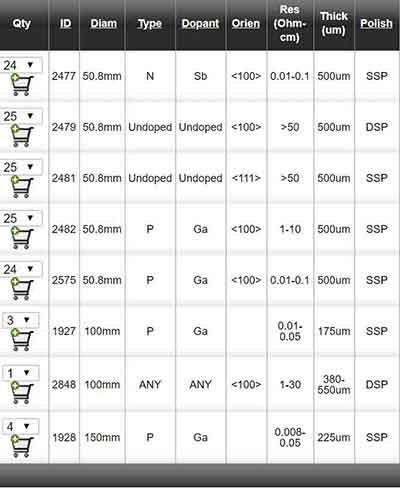
Ge Item #1927 - 100mm P/Ga 0.01-0.05 ohm-cm 175um SSP Orientation: <100> 6° towards <111> ± 0.5°uncoated ge wafer transmission data

I’m looking at using germanium wafers as windows for long-wave/mid-wave infrared experiment that I’m setting up. Based on the scale of the experiment I’m trying to get as large a window as possible. The information I’ve seen to date indicates that germanium has good transmittance, but I’m wondering if you can tell me how dopants like gallium might impact that infrared transmittance window. Specifically, I’m looking the spec above  – do you happen to have a transmittance spectrum for this product?  

Germanium Impurity Element

A scientis asked for the following quote:

I am looking for the below I am looking for the below 6" Ge wafer, Intrinsic Ge crystal Orientation (1 0 0) Concentrations of impurities must be less than 1E12 at/cm3 (1E10 is better) Q'ty: 1pc

Could you to provide the impurity data for our checking as this is main key parameter for us?

UniversityWafer, Inc. Quoted:

6" Ge wafer, Intrinsic Ge crystal Orientation (1 0 0) Concentrations of impurities must be less than 1E12 at/cm3 (1E10 is better) SSP,Thickness >/=350um,Resis. > 30 Ohm.cm,Q'ty: 1pc   

Please contact us for pricing.

Below is a Ge Impurity Element Table

The impurity atom is called five times the impurity, because the five valence electrons in the outermost shell share a free electron with the neighboring atom. Each electron has one electron at each atom, so the total number of free electrons at an atom increases with distance to each other.

Element Concentration (ppm wt) Element Concentration (ppm wt)
Li <0.001 Ag <0.01
Be <0.001 Cd <0.1
B <0.001 In <0.1
F <0.1 Sn <0.005
Na <0.001 Sb <0.005
Mg <0.001 I <0.01
AI <0.005 Te <0.005
Si 0.18 Cs <0.005
P <0.005 Ba <0.005
S <0.005 La <0.001
CI -- Ce <0.005
K <0.02 Pr <0.001
Ca <0.005 Nd <0.005
Sc <0.001 Sm <0.005
Ti <0.001 Eu <0.005
V <0.001 Gd <0.005
Cr <0.001 Tb <0.001
Mn <0.05 Dy <0.005
Fe <0.05 Ho <0.001
Ni <0.001 Er <0.005
Co <0.001 Tm <0.001
Cu <0.001 Yb <0.005
Zn <0.001 Lu <0.001
Ga <0.02 Hf <0.005
Ge Matrix Ta Source
As <0.2 W <0.005
Br <0.005 Re <0.005
Se <0.2 Os <0.005
Rb <0.005 Ir <0.005
Sr <0.005 Pt <0.005
Y <0.005 Au <0.05
Zr <0.02 Hg <0.005
Nb <0.005 TI <0.005
Mo <0.01 Pb <0.005
Ru <0.005 Bi <0.005
Rh <0.005 Th <0.001
Pd <0.005 U <0.001

Can Germanium Be Used As a Substitute For Silicon?

Researchers at Purdue University have developed a new compound that allows them to produce two different types of transistors. Previously, germanium was limited to producing "P-type" transistors. This discovery will allow scientists to create "N-type" transistors that are essential for CMOS circuits. Using this compound as a substitute for silicon will allow for greater efficiency and speed in semiconductor devices.

The transistor was created in the 1940s and changed the entire world. Previously, 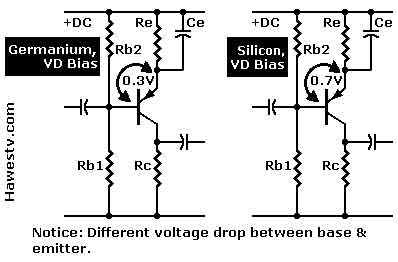different voltage drop between base and emitterelectronic devices such as vacuum tubes couldn't operate at higher frequencies, but the transistor changed that. Today, nearly every electronic device relies on transistors, including computer chips, which contain millions of transistors. These devices allow computers to perform operations, and they are a main component of computer chips. The first transistor was developed using germanium, and it quickly became a widely accepted semiconductor.

Although germanium is an excellent semiconductor material, the smallest transistors currently in production are 14 nanometers in diameter. According to Intel's senior fellow Mark Bohr, the semiconductor industry will be unable to achieve this goal for at least a decade. Nevertheless, if silicon's limitations can't be overcome, Germanium can be used as a substitute. But it's still not easy to make power-efficient circuits.

When it comes to transistors, Germanium was used in the first transistors. It was supposed to replace vaccum tubes in radars from World War Two. The military wanted something smaller, lighter, and more powerful. As time went on, this research became public, and commercial entities found that Germanium worked well in consumer electronics, too. Because silicon is more abundant than the former, it was cheaper and more widely used in a variety of consumer products. Despite its high price, Germanium is still widely used today, including in the ubiquitous transistor radio.

There are several advantages to using this material as a substitute for silicon in a variety of applications. For example, germanium's low cost makes it a cheaper alternative to titanium, which is often used in high-power circuits. Besides being cheaper, it's also less likely to degrade when processed in high-power devices. This material's lower cost makes it an ideal material for a wide range of electronics.

One major disadvantage of silicon is its high melting point, which is a major hindrance to using the material as a substitute for silicon. The latter has a higher melting point than germanium, which makes it more expensive. Therefore, germanium is a better choice for semiconductor devices. In contrast to the former, the latter is cheaper for manufacturers and for consumers. The latter. This is an advantage for the company.

The differences between silicon and germanium are quite striking. For example, the differences in the ICBO of the two materials can be huge, but it's not clear which is the better material for semiconductors. While both materials have similar electrical properties, they have different heat-resistant properties. When compared to silicon, germanium can be used as a substitute for silicon in certain applications. Further research is needed to determine which of the two materials is best for a particular application.

There are several ways in which Germanium can be used as a substitute. This new material is more efficient at conducting electricity and has some other desirable properties. Its low cost makes it a better option for a semiconductor, and its low thermal conductivity makes it a good choice for other electronics. A thin layer of germanium can also be used to create channels and increase the efficiency of a transistor.

In semiconductors, germanium can replace silicon in a number of applications. The use of germanium in transistors will allow for a smaller size. This is important for the manufacturing of many devices. In fact, some people believe that silicon is a good substitute for germanium in many applications. In the meantime, Germanium is a more affordable option. In this day and age, it is the most promising of the three materials.


Epitaxial Germanium for Electronic Devices

Electron transport in an Epitaxial Germanane is a fundamental characteristic of this semiconductor. In this article, we will discuss the structure of this material, the buckling parameter, and its applications. We will also discuss the underlying mechanisms that control the channel resistance and how they affect electronic device performance. We will also discuss the benefits and limitations of Epitaxial Germanane for Electronic Devices. After reading this article, you should be able to answer the question, "How can this material be used to create a semiconductor device?"

Structure

Using a structure of epitaxial germanane as a semiconductor, you can tailor its electronic properties. The band gap of germanane is almost unchanged despite doping with a p-type dopant. However, an external E-field can change the band gap by promoting p-type doping. This allows you to create an electronic device that is more functional than conventional semiconductors.

To understand this effect, you can map the electron mobility of germanane in a thin layer. Then, you can see the valence band corresponding to the different energy levels below Fermi's level. Lastly, you can measure the back-gate voltages of three different devices at 300 K and see how they change. These results are based on the data obtained from the above-mentioned studies.

The structural characteristics of the germanane framework are determined by XRD and Raman spectra. From the second major reflection, the a-lattice parameter, a-lattice, can be calculated. It depends on the length of the Ge-Ge bond and its angle. In other words, the longer the Ge-Ge bond, the greater the a-lattice parameter.

Electron transport

Epitaxial germanane is a material that can be transferred onto an arbitrary substrate by an electrochemical delamination process. The resulting films are of varying thicknesses ranging from one to six hundred nanometers. The layers of this material are separated by an interlayer distance of about five centimeters. Various characterization methods are available to confirm this property. They include x-ray diffraction and photoluminescence. The resulting films are also highly insulating with a transition from insulator to metal.

Despite the fact that conventional semiconductors and epitaxial germanane are dimensionally large and have a limited band gap, germanane's direct band gap makes it an excellent material for optoelectronics. Electron transport in this material is dominated by the s bond, which is composed of px and py orbitals. The s bond is thought to be stronger than the p bond, allowing for spin-selective optical processes.

Buckling parameter

The buckling parameter is the separation between the germanene's triangular sublattices along the c-direction. This property is controlled by the competition between the elastic and electronic energies. It is 0.65 A in the monolayer germanene density functional theory. This material has an essentially zero density of states and a high density of s-orbitals.

Using the buckling parameter of epitaxial germanane to measure SOI, we found that the resistance of the annealed germanane decreases drastically. At 210 degC, the resistivity drops drastically. It also loses its ability to tune its source-drain current, which is essential for electronic devices. Instead, a stronger ionic gating technique is needed to tune this parameter. However, this technique only slightly tunes the IDS.

The germanene structure was first mapped out through a high-resolution synchrotron-radiation-based photoemission experiment. Next, a single monolayer of germanium was annealed at 250 degC for 10 minutes, followed by STM imaging and low energy electron diffraction. From there, we performed detailed core-level spectroscopy analysis.

Applications

The formation of epitaxial germanane thin flakes requires a process of mechanical exfoliation. The material is stable under an inert gas atmosphere or ultrahigh vacuum, but is highly reactive with oxygen. To develop thin flakes, germanane bulk crystals were mechanically exfoliated on a highly doped Si substrate, then coated with 300 nm SiO2.

Typical properties of epitaxial germanane films include direct band gap properties and bilayer structure. The band structure of the germanane crystal is optimized using a density functional theory code called VASP. The energy cutoff for the VASP calculations is 600 eV, and van der Waals interactions between the layers are accounted for using the Grimme DFT-D2 method. At 210 degC, the resistance decreases dramatically. This metallic behavior is accompanied by a loss of tunability with an electric field.

The optical properties of germanane have been studied using diffuse reflectance absorption spectroscopy. The material exhibits broad absorption over the visible range, and a linear approximation of the absorption edge suggests a band gap of approximately 1.59 eV. However, a tauc/Davis-Mott expression predicts a step function near the band edge and a discontinuity at the band gap. This is consistent with a large band gap that is directly proportional to energy.

How to Write the Electron Configuration for Germanium (Ge)

What do you know about the valency of germanium? Germanium is a valency two element. In other words, it has two electrons per atom. Let's start with a definition. Germanium is a semiconductor that has two electrons. Its valency is 2 and it is a type of metal. Hence, the name. Listed below are some of its properties.

d5 d 5 configuration

One important part of a chemical equation is the valency of an element. If a material has a valency of two, it will have a certain electron configuration, or orbital structure, and this configuration must be written. You can see this information by looking at a germanium orbital diagram. This diagram can help you understand the relationship between the valency and electron configuration of a substance.

The electron configuration of a chemical element is called the 'atom's' electron distribution. For example, the atom of oxygen has an atom with four electrons in its outer shell (shape), while the atomic configuration of nitrogen is 1s22s22p3. When it comes to the atom of germanium, the valence electrons are two-thirds of a single atom and are distributed evenly throughout the atom.

What is the Aufbau Principle?

The Aufbau principle states that an atom can have many electrons. This is because a molecule can have more than one electron in any given orbit. Hence, the atom's orbital configuration is required to maintain the atomic structure. The Aufbau principle states that electrons are assigned to orbitals with different energy levels. The electrons that are added to an atom first enter its lowest energy orbital, which is's'. This is followed by a gradual filling of higher energy orbitals.

The solid state structure of Germanium is Face Centered Cubic. The atomic positions of Germanium are measured from the reference point (or Lattice Angle) in each unit cell. Space groups are used to describe the symmetry properties of a crystal, and the 230 different space groups are used to describe the possible symmetric arrangements of particles in three-dimensional space. This structure allows scientists to study the behavior of the Germanium crystal.

3d54s1

The electron configuration for germanium is written in the form of two parts, a complete configuration and an abbreviated configuration. In writing an orbital diagram, you will need to know the electron configuration of the element. You can write the Germanium electron configuration two ways: in the short form, with a hyphen and no hyphen, and in the abbreviated form, with a minus sign.

The atomic number of Germanium is 32 and the symbol for the element is 'Ge'. The element has four electrons, two of them valence and two stoichrome. You can write the electron configuration of germanium with the help of a chemical formula. The electronic configuration of this element can be calculated using the formula 'E=mc2'. The valence electrons are in the top row, while the other two electrons are in the bottom row.

3d54s2

To properly read an orbital diagram, you need to know how to write the electron configuration for germanium. The valency of germanium is two. The valence of the electrons is equal to the number of protons that occupy the orbital. The electron configuration of germanium is 'l'. To write the orbital configuration for germanium, you must know the valency of the other elements.

First of all, you must know the symbol of germanium. Its symbol is 'Ge'. This means that there are four electrons in this element, including two valence electrons. This means that the atoms in germanium are in a two-dimensional configuration. This is the same way that the electron configuration of other elements is written, so this method is useful to write down the electron configuration of germanium.

3d54s3

The electron configuration of germanium is an important part of the orbital diagram of the element. To understand how the electrons in germanium are arranged, it is important to know its valency, or charge. For instance, a metal atom has two electrons in its shell, which is called the valence. To write the orbital diagram of this element, you must first understand the electron configuration of germanium.

The solid state structure of Germanium is a Face Centered Cubic, and this crystal is described using the concept of a unit Cell, or cube. The atomic positions of each individual atom within the unit cell are measured in relation to a reference lattice point. In order to understand the symmetry properties of the Germanium crystal, we must understand the concept of space groups, which describe the different symmetric arrangements of particles in three-dimensional space.

Video: How to Write the Electron Configuration for Germanium

What is Germanium (Ge) Orbital Notation?

In the Atomic orbital structure of a particular element, the electrons are bound to certain configurations. This is the case with Ge. It belongs to the group 14 in the modern periodic table. Specifically, it has ns2np2 and 4s24p2 as the outer electronic configuration. Listed below are the electron configurations and binding energies of Ge. This article will cover these topics and more.

Germanium's Atomic Orbital Structure

The atom's structure is determined by its electrons' relative energies. When an element has more than one electron, its angular quantum number is increased and the energy of different subshells increases. The energy of each subshell is governed by the shape and size of an orbital. The s orbital always has the lowest energy. This is the reason why it is called the's' orbital.

The spin quantum number, ms, differentiates two electrons in an atomic orbital. ms can be -1/2 or +1/2. If there are two electrons in the same orbital, their spins must be opposite, but the first three 'qubits' will be the same. An atom can have a total of four electrons if it is composed of two unpaired electrons.

The energies of different atomic orbitals are described using the principal quantum number, n. The lower-energy's' orbital has the least energy. The higher-energy 'n' orbitals have more energy. This energy increase cannot be predicted. The order will be explained through various methods. We will explore the different methods to memorize this information. There is a simple device to estimate the relative energies of atomic orbitals. A table is constructed using the allowed combinations of n and l quantum numbers. The arrows point in the direction of increasing energy of the orbitals.

The s-orbital is the most commonly used method for describing the orbital structure of an element. In this way, electrons can be seen as separate sub-atoms. The valence number of an element is defined by the configuration of electrons in its excited state. In the case of Ge, this is s = 3; f=4, n=3, r=0, and c=10.

What are Ge Electron Configurations?

If you want to study the structure of atoms and their electron configurations, you need to understand the concept of d-block orbitals. Essentially, these are electron configurations that have a different number of protons than they do neutrons. You will find that this type of notation is based on the electron configurations of the d-block elements. For example, the electron configuration of the d-block element is 2s4, while that of the s-block is 4p2. If you are studying this structure, you should be able to read the corresponding table.

The m-block of electrons is the second smallest unit. If there are three electrons in an 'l' orbital, they are considered degenerate. For example, a 'l' orbital has two protons and three electrons. Therefore, a 'l' orbital has two protons and one electron. In addition, the orbitals of the 'd' and 'p' shells each have a total of eight electrons.

The m-block orbital notation is also based on the electron configuration of the atom. The electron configuration of sodium has a single proton, while that of lithium has two. In a similar fashion, the m-block is characterized by an electron density of 0.425. This means that sodium and lithium have identical electron configurations. In addition, both atoms are alkali metals, so they have one electron in the valence s subshell.

What are Germanium Electron Binding Energies?

The basic unit of Ge orbital notation is the electron. Unlike most other atomic systems, the electrons of a given atom are separated into three subshells: the 1s, 2s, and 2p. The 1s subshell is the most closely associated with the nucleus, and is thus shielded the least. In this way, the electrons in this subshell have the highest binding energy, followed by the 2s, and so on.

The electron binding energies of Ge are quoted in eV and are relative to the Fermi level for metals and the top of the valence band for semiconductors. Ge orbital notation for electron binding energies is based on data provided by Gwyn Williams and are adapted from references 1-3. The data have been tabulated in paper form. However, this doesn't mean that the electron binding energies of Ge are inherently higher than those of metals and rare gases.

For weakly bound systems, the best method is an allometric approximation. For this, we need a basis set that is exceptionally diffuse. Skurski et al. recommend using aug-cc-pVDZ basis sets and even-tempered extrapolation for ground-state calculations. These methods work well for weakly bound systems, but are not universally applicable.

What is the Atomic Orbital Structure for Germanium?

The Germanium atom has four coordinates. Its orbital structure is trigonal planar, and the angles around it are 355 degrees. The length of the Ge-N1 and Ge-N2 bonds is 2.050 and 1.884 degrees, respectively. The length of the Ge-S bond is approximately 1.386 degrees, comparable to that of diarylgermanethione. This structure allows atoms in adjacent orbitals to interact with each other through a hydrogen bond.

The p-orbital contains three sub-orbitals: px, py, and pz. Each sub-orbital can have a maximum of two electrons. As we mentioned earlier, the atom of germanium has four electrons in its ground state. The electrons in this orbital configuration are arranged in a hexagonal shape, forming a hexagonal structure.

The first use of the Germanium element was as an electrical component. This element was used in electronic devices in 1872, replacing the diode, the most basic electronic component. It contained a heater for emitting electrons, and an anode for collecting them. Its electrical conductivity can be altered by external influences, which makes it an ideal material for semiconductor devices. There are no known harmful effects of the Germanium element, and its use in electronics is growing every day.

The Aufbau method consists of electron configurations through a sub-energy level. The Aufbau principle states that electrons in the same atom will first fill its lowest energy orbital, and then progress through higher energy orbitals. The atom has four types of electrons: s, p, and d. Similarly, the f-orbit has one type of electron, but the spin of the electrons is in the opposite direction.

What is a Germanium Ion?

In the field of chemistry, ion orbital notation is the most commonly used method to describe a substance. Germanium is a naturally occurring metal with four stable isotopes. These are listed below. The first step in understanding ion orbital notation is to learn more about this metal's chemical properties. This article will go over the properties of germanium and give you a basic understanding of the notation.

The ion orbital configuration of germanium atoms is 1s2 2p6 3d10. Its oxidation state can change from +2 to +4 depending on the formation of a bond. It is important to note that the ion orbital notation is not the same for all germanium elements. You should look for the electron configuration of germanium atoms in each of the sub-orbitals to make sure that you're understanding the atom's valency.

For those who are unfamiliar with the periodic table, Germanium is an element in the fourth period. The chemical element is placed at position 32 in the periodic table and is a metalloid. The metalloids, which are intermediate between metals and nonmetals, fall into the fourth period. While the metalloid Germanium is a part of the carbon family, it shows similarities with the neighboring elements antimony and arsenic.

What are Germanium Ion Isotopes?

The periodic table of elements shows the atomic number of elements, and Germanium is no exception. Germanium is a transition metal that is in the same family as silicon and carbon, and has an orbital structure that goes from 2-8-18-4. The atomic number of Germanium is 32. The metal is found in two main groups, which are referred to as periods and rows.

When an atom absorbs energy, it moves from its ground state to an excited state. The excited state of the atom determines the valency of the element. Since germanium has four unpaired electrons, it has a valency of four. Unlike most other elements with only one unpaired electron, it does not have a valency of seven. The valency of germanium is a number which is determined by the atomic number.

A stable element like germanium usually has several stable isotopes. These isotopes share the same atomic number but differ in the amount of neutrons. Germanium isotopes 74Ge, 72Ge, and 76Ge all have similar properties but differ slightly in their orbital notation. Among these, 76Ge is radioactive and decays through double beta decay. Germanium-70 is the most abundant isotope, containing 32 protons and forty neutrons.

This model is based on an analysis of experimental nuclear moments of germanium around N = 40. It uses large-scale shell-model calculations in the f5/2 pg9/2 model space. The calculated wave functions show a mixed configuration with unpaired neutrons. This systematic comparison of nuclear moments reveals a gradual increase in collectivity as protons are added to the Z = 28 closed shell and

Germanium (Ge) Valence Electrons

How Are Germanium Valence Electrons Produced?

If you want to learn more about germanium valence electrons, you can read this article. This article will explain how germanium's electrons are formed and how the valence electrons in this metal are positioned. This article also includes an image of the germanium atom in an electron cloud. This atom cloud has two kinds of electrons: valence electrons and conduction-emission electrons.

An atom has an equal number of protons and electrons and is characterized by discrete bands of energy. The valence band is made up of the atoms of silicon, germanium, and bismuth, and there is one extra electron in these materials. This extra electron does not participate in bonding and is referred to as a minority carrier. Another way in which germanium valence electrons are produced is by adding a trivalent impurity atom to intrinsic silicon. This increases the number of holes in the semiconductor.

Video: Germanium Valence Electrons

What is Dislocation Free Germanium?

Dislocation free Germanium is an important metal for electronic applications. The dislocations are stable, react with each other and have a high energy. It has high electron mobility and is a promising candidate for use in high-frequency RF circuits. In addition to being stable, dislocations are energy-friendly.

Dislocations are stable

The structural properties of dislocation free Germanium are stable in high-temperature conditions. This is due to preferential porosification that increases atomic mobility and allows preferential diffusion paths for voids and dislocations. This phenomenon can be observed in Ge epilayers grown on Si.

The study reveals that Germanium SEG leads to a high-purity germanium crystal with a dislocation density of about 3000 cm2/cm2. The topography of the crystal revealed clusters of vacancies. This observation was confirmed by examining the dynamical diffraction effect. Moreover, dislocation density analysis performed using etch pit density failed to adequately represent dislocations in the dislocation-free regions. As a result, a different type of dislocation free Germanium is formed.

The energy spectrum of Germanium dislocation states is extremely complex. The structure of the energy spectrum of dislocation free Germanium enables the calculation of its stability. The corresponding theoretical curves are compared to the experimental curves. This study suggests that dislocation free Germanium is stable in high temperatures.

Moreover, dislocation density can be controlled to a certain extent. This is important for detector requirements. However, etch pit density analysis is not always reliable. An alternative method of determining the dislocation density is x-ray topography. This technique reveals the actual dislocation density of the material and whether it contains voids.

They are energetically favorable

High-resolution transmission electron microscopy (TEM) studies have revealed the crystal structures of Ge/Ge x Si1-x/Si heterolayers doped with quantum dots. As illustrated in Fig. 16, the layers of germanium, silicon, and solid solution are in contrast. Moreover, the structure is elastically strained, and the germanium islands do not undergo plastic relaxation. This results in a hut cluster-like structure.

Strain engineering has also been used to modify the band structure of germanium on silicon to enhance its optoelectronic properties. When the germanium film cools from its high growth temperature, a thermally induced tensile strain of 0.2% occurs. This strain allows the bandgap difference of Ge to fall from 136 meV to 110 meV. Moreover, bandgap engineering on silicon wafers has enabled the emission of Ge light.

Epitaxial growth of germanium on silicon yields two and zero-dimensional planar films. It is dependent on different growth mechanisms and material parameters. The crystal structure of SiGe influences the growth process and the energy levels in layers. The surface tension and interface energy are important factors for the growth of germanium on silicon. Achieving a flat layer of germanium on silicon requires careful control of surface roughness. In addition, it is necessary to avoid threading dislocations in the surface layer.

They are free

Dislocation-free germanium crystals exhibit a distinctive yield behavior over a wide temperature range. The highest and lowest test temperatures are similar, and the stress-strain curves show that maximum stresses decrease exponentially with increasing temperature. The flow stresses follow a relationship of t = A exp (E/kT) over a range of strain rates.

Dislocations have a major impact on the electrical properties of germanium. The dislocations are known to act as electron acceptor centres. One of the simplest models of dislocation acceptors was proposed by W. Shockley, in which the dislocations are dangling unpaired electrons in extra atomic planes. These electrons become negatively charged in n-type germanium. The electron concentration in n-type germanium is determined by the temperature and electrostatic energy of the material.

Dislocation-free germanium crystals have a high crystalline perfect-ness and low dislocation density. This is important because highly sensitive detectors require germanium crystals with high crystalline perfection and low net charge carrier density. The presence of voids, dislocations, and defects can cause poor sensitivity.

They react with each other

Growing high-purity single crystals of germanium is one of the main challenges in the growth industry. Single crystal quality depends mainly on dislocation density. This parameter is measured using a Czochralski technique. Numerical simulation of germanium crystal growth using heat-transfer and hydrodynamics models is also used. This model can help to understand lattice defects in germanium crystals and improve the quality of single crystals.

Different types of germanium bicrystals exhibit similar but distinct dislocation structures. They both have stacking fault-like structures with interfacial dislocation networks. The dislocation grid of germanium bicrystals consists of a honeycomb network of parallel partial secondary dislocations and a perfect secondary dislocation. The parallel dislocations cross one another. Partial dislocations are common to the two crystals, which suggests a boundary between the two crystals.

For optimal Germanium chemistry, it is important to grow epitaxial layers. Molecular Beam Epitaxy and Chemical Vapour Deposition are common epitaxial deposition methods. Recent advances in the field of epitaxial growth include Atomic Layer Deposition and Low Energy Plasma-Enhanced Chemical Vapour Deposition (LEPEC) methods.

They move easily

Germanium is a rare element in the Earth's crust. Its cosmic abundance is approximately equal to that of beryllium, molybdenum, cesium, antimony, mercury, and krypton. Its relative abundance is slightly lower than those of heavy elements such as lead, mercury, and arsenic.

Its ability to move electrons and holes easily makes it an ideal material for semiconductors. The material is three times as mobile as silicon, allowing it to create circuits much faster. It also consumes less energy than silicon. This makes it an excellent material for CMOS circuits, which make use of two different kinds of transistors.

Germanium's low energy density makes it easy to incorporate into silicon chip manufacturing processes. Researchers are also hoping to use this material to make computer chips that use light instead of electricity. The researchers have developed a laser made of germanium that emits wavelengths useful for optical communication. This material is also a promising material for optical computing, as it is easily incorporated into silicon chip manufacturing.

While germanium is the most common semiconductor material, its energy band gap of 0.72ev is smaller than that of silicon. This makes it a key material for increasing chip performance. However, it is not the only high-mobility material. Other III-V compounds, such as indium arsenide, also have high mobility. Indium arsenide has electron mobility that is 30 times greater than that of silicon. Unlike silicon, indium arsenide has no holes.

They react with swirl defects

In order to achieve low dislocation density in a Ge device, it is important to tune dislocation motion. To do so, the Ge epilayer must be re-solidified. By doing this, the dislocations will bend toward the Si voids, which will facilitate TD recombination. This approach is compatible with modern microfabrication techniques.

Swirl defects were first discovered in the seventies in large dislocation-free Si crystals. They come in two forms, known as A-swirl defects and B-swirl defects. These defects are visible when the illuminating source is angled towards the crystal. Light scattered by the swirl defects enters the camera lens, forming a spiral pattern.

Usually, we gain knowledge about defects from diffusivity experiments. For example, interstitial atoms that are not covalently bound to silicon diffuse easily. But atoms with covalent bonds have lower diffusion coefficients. Furthermore, substitutional atoms have lower diffusivities than IV-group donors.

The theory of dislocation motion is based on Koehler's theory, which states that a dislocation's motion is determined by a point defect's motion. This effect is observed in the Cottrell potential, which is the interaction between the dislocations and point defects.

They are prone to failure

Dislocations are a fundamental property of all crystalline materials, and they form ramps and steps on the surface of a crystal. They also play an important role in the growth of one-dimensional nanowires. The presence of dislocations was originally used to explain the growth kinetics of spontaneous nanotubes.

The density of dislocations is a property that can be controlled to a certain extent. However, it is essential to have a reliable method for determining dislocation density for detector applications. For example, etch pit density analysis is not always reliable. An alternative method of determining dislocation density is x-ray topography, which can accurately show dislocation density and the presence of voids in the dislocation-free parts of the crystal.

Video: Germanium Dislocation Explained

What Is the Resistivity of Germanium?

To determine the resistivity of a material, you need to know how it reacts to voltage and current. You can find this information by consulting Table 1 below. Table 1 also gives the resistivity of various materials, including germanium. This material has a low resistivity and is usually used in electronics and electronic components. The resistance of germanium is about 6 million ohms/cm.

Table 1

The resistivity of germanium is a very important property when fabricating devices. The production process germanium resistivity graphspeed and the solid-liquid interface affect the resistivity distribution, which directly affects device reliability and yield. One of the most common methods for measuring the resistivity of semiconductor materials is the DC linear four-probe method, which is widely used by semiconductor materials researchers.

The resistivity of a material increases with temperature. Most metals exhibit a positive temperature coefficient of resistance. In contrast, the temperature coefficient of resistance of manganin is nearly zero, and it can therefore be used to develop a temperature-independent resistance standard.

EC - EFn

The resistivity of a material is a measure of its ability to transfer a current. It is the inverse of electrical conductivity, and the lower the resistivity the easier it is for an electric current to flow. It is usually represented by the Greek letter r, and the unit used to measure it is the ohmmeter. In a circuit, this property is useful in determining the efficiency of an electrical connection, which is crucial when it comes to power supplies.

Pure germanium has a resistivity of 60 ohm centimeters, which is equivalent to that of silicon. When impurities are present, this resistivity can be reduced or increased. These doped semiconductors are used in infrared spectroscopy, electric guitar amplifiers, and camera lenses. Doping is classified into two types: n-type and p-type. N-type doping adds extra valence electrons to a semiconductor. The extra electron is called an excess electron, and it is impossible to form electron bond pairs with the remaining electrons.

EC - EF

Germanium is a semiconductor, similar to silicon, with a resistivity of 60 ohm-centimeters. This resistivity decreases as the temperature rises and depends on the presence of impurities. This property makes germanium useful for applications in solid-state electronics, including electric guitar amplifiers, camera lenses, and infrared spectrometers. While it is a rare element, its use has increased over the years, largely due to the invention of doping.

The resistivity of germanium is also known as specific resistance or volume resistivity. This property determines how easily electric current flows. The lower the resistivity, the easier it is for current to flow. The resistivity of germanium is measured using an ohmmeter.

EC - EFn3

Electrical conductivity, or EC-EFn3, is the strength of a substance's ability to conduct an electrical current. Resistivity is measured in ohms, with a high value indicating that the material is highly conductive. A lower resistivity means that the material readily allows an electric current to flow. The EC-EFn3 resistivity of germanium is the lowest of all metalloids. It is a hard, brittle metalloid that is chemically similar to silicon.

The EC-EFn3 resistivity of germanium is about 60 ohm-centimeters for pure germanium, and 60 ohm-centimeter for doped germanium. EC-EFn3 resistivity of Germanium decreases with temperature. It also depends on whether the metal has impurities. The EC-EFn3 resistivity value of Germanium is used in semiconductors in electronic devices.

EC - EFn4

The EC - EFn4 resistivities of germanium are closely related to those of semiconductors. They are determined by measuring the resistance of a substance to electric current. The higher the resistance, the more difficult it is to conduct electricity through the material. The resistivity of a material is expressed as the ratio of its internal resistance to its volume.

The electrical grade of Germanium is a great choice for solar cells because it has good conductivity. It is often doped with g-germanium (G) and is cut into thin films. It is inexpensive and can be used in many different types of applications. This includes solar cells, transistors, and batteries.

EC - EFn5

The EC - EFn5 resistivities of germanium and their relation to temperature are studied. In general, the higher the resistivity, the more conduction the material will be, and the lower the resistivity, the lower the resistance. However, it is important to note that a single measurement of resistivity may not always give the most accurate answer.

Resistivity is a useful property to know when comparing two different materials and comparing their electrical conductivity. It is defined as the resistance of a cube with edges of unit length when a current flows along its opposite faces. In general, the resistivity of a material is measured in Ohm metres, where an Ohm is a measurement of one metre in each direction.

EC - EFn6

The EC - EFn6 resistive characteristic of germanium is dependent on the amount of impurities present in the material. If the element is doped, it can become less resistive and increase its electrical conductivity. This is done to improve electronic properties in semiconductors. Examples of doped germanium are camera lenses and infrared spectrometers.

The EC - EFn6 resistive property is a useful tool for measuring electrical conductivity. The EC - EFn6 value of germanium is the inverse of its electrical conductivity, and its low value means that an electric current flows freely. The unit for measuring resistivity is the ohmmeter.

EC - EFn7

Resistivity, also known as specific resistance, is the inverse of electrical conductivity. The lower the resistance, the easier it is for electric current to flow. The unit of resistance is an ohmmeter. Germanium exhibits low EC - EFn7 resistivity values, which are indicative of its semiconducting properties. Its chemical properties are similar to those of its neighboring metalloid, silicon.

EC - EFn7 resistivities of germanium tend to be less than those of silicon. However, it is possible to lower the resistivity of germanium by adding other substances to it. This makes the material more conductive, which makes it a valuable material for electronics.

EC - EFn8

The EC - EFn8 resistive properties of germanium are reflected in the EC-EFn8 value. The higher the resistivity, the more difficult it is to conduct electricity through it. Because of this, the EC-EFn8 value of germanium is important for the development of solid-state electronics.

The EC-EFn8 resistivity of germanium is very high. Therefore, if you are looking for a high-quality component at a low cost, you should opt for a high-quality one made of high-quality materials. A high-quality, high-performance component will last for years.

The EC-EFn8 resistivity of germanium is an important property for determining the metal's oxidation resistance. This property is measured in volts.

EC - EFn9

The EC - EFn9 resistive characteristics of germanium are the inverse of its electrical conductivity. It is an important parameter to understand as it is a measure of how well a material allows the flow of electric current. The EC - EFn9 resistivity of germanium is relatively high and therefore the conductivity of this material is low.

Germanium is a cheap metal that can be used in many applications. It is often used in thin-film solar cells and can be incorporated into a wide range of electronic devices. Because it is so inexpensive, it is a popular material in solar cell manufacture.

Video: Germanium Resistivity

Why is the Band Gap of Silicon More Than Germanium?

The energy gap of Ge and Si increases as the pressure increases. The difference is attributed to the pressure germanium vs silicon bandgapcoefficient (a), which is negative for Si and positive for Ge. In both cases, a depends on the type of transition. In Ge, a is about 5 meV/kbar; in Si, it is -1 to -2 meV/kbar. This negative value is attributed to the strong influence of the d levels, which lie above the X maxima of the conduction band.

Silicium

Silicon and germanium are two Group IV elements that share four valence electrons. This arrangement would allow the two elements to have a larger outer shell, with eight electrons total, which would increase the stability of the atom. Despite the fact that these two materials are very similar in structure, they are incompatible as semiconductors because their valence electrons are not in the same arrangement.

The difference between the two materials comes from their different band gaps. These band gaps are determined by the difference in energy between their bonding and antibonding orbitals. For instance, carbon has a wide band gap because the C-C bond is very strong. In addition, the thermal energy available in room temperature is insufficient to excite electrons from a filled band to an empty one.

Increasing pressure increases the energy gap in Ge while decreasing it in Si. This difference is reflected in the pressure coefficient (a) of the two materials. In the case of Ge, the pressure coefficient (a) is positive while in Si, it is negative. This difference is due to the difference in the Gv-Lc transition coefficient, which is five meV/kbar in Ge and one to two meV/kbar in Si.

In the periodic table, pure silicon has a higher band gap than pure germanium, while germanium has a lower one. Silicon, on the other hand, has a lower melting point than germanium.

Germanium

The band gap is a measure of the difference between the energy levels of two semiconductors, such as silicon and germanium. The band gap of silicon is 1.12 eV, while the band gap of germanium is 0.75 eV. Both materials are common in modern electronics.

This difference is caused by the differences in size between the atoms of silicon and germanium. The silicon atoms are smaller than those of germanium, which means that their electrons are more tightly bound to the nucleus. In contrast, the germanium atom electrons are loosely bound.

The difference in bandgaps is important in semiconductor design. When two semiconductors are used in a solar cell, their bandgaps need to be in the same range. In order to be effective in solar cells, a semiconductor should have a bandgap of one to 1.7 eV. Silicon is the better semiconductor for solar cells due to its higher bandgap value.

Another important difference between the two semiconductor materials is the difference in energy levels. At room temperature, silicon has the largest forbidden energy gap, while germanium has the least forbidden energy gap. At high temperatures, the energy gap between silicon and germanium is almost equal, enabling electrons to easily transfer between the two.

A negative pressure coefficient in Si affects its energy gap, but it is not the same for Ge. The higher the pressure, the higher the energy gap.

InGaP

If you look at the periodic table, you will notice that silicon and germanium have slightly different band gaps. The difference is in the size of the atoms. Because silicon and germanium are smaller, their electrons are more tightly bound to their nucleus. As a result, they have a larger band gap than their counterparts.

The band gap of Si and Ge increases with increasing pressure, while it decreases with increasing temperature. The difference between their band gaps is due to a pressure coefficient (a) that is positive in Si and negative in Ge. This coefficient depends on the type of transition, and the Gv-Lc transition in Ge has an a-value of 5 meV/kbar, while the Gv-Xc transition in Si has an a-value of -1 to -2 meV/kbar. This difference can be explained by the strong influence of d levels, which lie above the X maxima of the conduction band.

In order to determine whether the band gap of a given material is wider or narrower, we need to calculate the band structure. This band structure is a measure of how much energy is present in the valence band compared to the conduction band. This information provides valuable insight into the properties of optical devices. Ideally, a semiconductor band structure would be filled with electrons and have an empty band. This is the ideal state, and a gap of one or more electrons separates these two regions.

The energy gap between the two bands depends on the strength of bonds between atoms. A small difference in energy allows electrons to transfer from one band to another. Generally speaking, the energy gap between the two bands is equal to one. In the case of silicon, the energy gap is 1.1 eV, whereas the band gap of germanium is 0.78 eV.

111 sandwich structure

The band gap of silicon is larger than that of germanium, and the 111 sandwich structure can be described by using a model of oxidized bilayer silicene on an Ag(111) substrate. This model has a SiOx buffer layer between the silicene top sheet and the substrate below. The top silicene sheet retains its hexagonal honeycomb lattice and has weak interactions with the SiOx buffer layer. This weak interaction between the silicene sheet and the substrate leads to the simulated STM image.

A dirac cone structure is also present in this structure, and is assigned to linear p states of three x three silicene. This Dirac point is positioned at 0.33 eV below the Fermi level. The electrons that dop the silicon come from the Ag(111) substrate.

The bandgap of silicon is higher than that of germanium because it contains more hydrogen than germanium. However, this does not mean that the two metals cannot exist in combination, as it is common to have some metal bonded to silicon. Both of these metals are important for the electrical conductivity of semiconductors.

Oxygen intercalation has a significant impact on the electronic structure of silicene layers. For example, Figure 4 shows the electronic band structures of pristine silicene and oxygen-intercalated silicene grown on Ag(111). The BZ center and the bulk Ag sp band are visible, as are two faint bands with linear dispersion crossings at the G point.

Tunneling FETs

Silicon and germanium have different properties, which makes them a good match for different semiconductor applications. For example, silicon has a larger bandgap than germanium. However, this difference is only a small factor. The largest differences are in the atomic numbers and the relative electron masses.

In tunneling FETs, the electric field around the gate controls the flow of electrons. The amount of electrons in this region depends on the gate voltage. When the gate source voltage is high enough, the BTBT probability becomes high. Silicon, on the other hand, has a lower probability of BTBT.

Tunneling FETs are a great way to improve transistor performance and improve energy efficiency. The smallest ones have the highest energy band gap, but they are more expensive. They are also more prone to failure. A recent study on a nanotube tunnelling FET has shed more light on the problem.

The high hole mobility of germanium is linked to defect density. In addition, the germanium layer has an anisotropic surface reconstruction, resulting in twins in epitaxial layers. The resulting GeSn alloys also have a higher hole mobility than silicon. The performance of these alloys as channel materials is summarized in Figure 1.43. In addition to the increased hole mobility, GeSn alloys also show higher saturation drive currents than Si.

Another disadvantage of conventional silicon TFETs is its large bandgap. This limits electron band-to-band tunneling. Moreover, the silicon-based TFETs have several critical problems, including a low on-state current. However, this has led to research on improving these devices.

Optical band gap

The energy gap of silicon and germanium crystals is evaluated at different temperatures and pressures. The variation of Eg with temperature and pressure is analyzed using different equations of state. The results of these calculations are consistent with experimental results and previous theoretical calculations. They also show the QC effect.

A single-step method has been developed by researchers at the University of Surrey to create strain in semiconductors and alter their band structures. The indirect band gap of silicon semiconductors limits their light-producing ability, whereas the direct band gap of compound semiconductors allows electrons to easily lose energy when producing photons.

The difference between these two semiconductors is caused by the size of their atomic nuclei. Silicon has a smaller atomic number than germanium, which means its electrons are more tightly bound to its nucleus. Hence, the band gap of silicon is higher than that of germanium.

When light passes through a semiconductor material, it passes through a thin membrane. The energy of the photons is small, but the energy of the phonon is large enough to knock an electron out of its valence band. In contrast, photons of visible light have energies of 1.6 to 3.2 eV, so a single photon of sunlight can knock an electron out of silicon's valence band.

The optical band gap of silicon is more than that of germanium because of the difference in electron mobility. When the energy of an electron increases, it will be promoted to a higher energy level. This process is called a transition. This transition allows electrons to move freely within the crystal lattice and is crucial for conducting electric current.

Video: Bandgap Explained

 

What is Ground State Electron Configuration for Germanium?

The ground state electron configuration for an atom describes the distribution of electrons in its atomic orbitals. Germanium (Ge) has 32 electrons, as it is the 32nd element on the periodic table. To find its ground state electron configuration, we can build up the configuration by adding electrons to the atomic orbitals in accordance with the Aufbau principle, which states that electrons are added one at a time to the lowest energy orbitals available until all of the electrons have been placed in an appropriate orbital.

Using this principle, the ground state electron configuration for germanium is:

ground state electron configuration for germanium

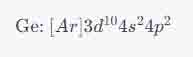
This notation means that germanium has the electron configuration of argon [��] plus ten electrons in the 3d orbitals, two electrons in the 4s orbital, and two electrons in the 4p orbitals. It's important to remember to fill up the 3d orbitals before moving on to the 4p orbitals, as 3d orbitals are of a lower energy level than 4p orbitals.