Get Your Quote FAST!
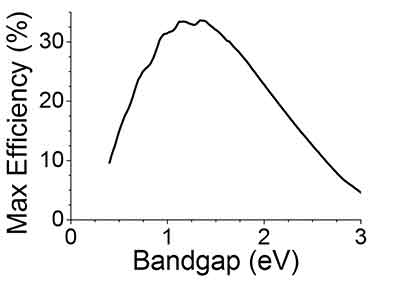
The Shockley-Queisser limit is a theoretical upper limit for solar cells. The actual maximum solar cell efficiency varies with the temperature of the solar cell. For example, the maximum Shockley-Queisser limit for a single junction solar cell is 33.7%. By contrast, a single-junction solar cell with a band gap of 1.5 eV produces only 337 Wm-2 of electrical energy, which is significantly below the Shockley-Queisser limit for blackbody radiation of 6000 K.
Get Your Quote FAST! Or, Buy Online and Start Researching Today!
Graph: Maxium Solar Efficiency of one p-n junction solar cell
What Substrates are used in Shockley Queisser Limit Research?
The Shockley-Queisser limit, which is a theoretical limit for the efficiency of a single p-n junction solar cell, involves research on a variety of substrates. The choice of substrate largely depends on the material and technology used in the solar cell. Common substrates include:
-
Silicon (Si): Silicon is the most commonly used substrate in solar cells, including those studied for the Shockley-Queisser limit. Silicon is popular because it's plentiful, safe to handle, and its properties are well known.
-
Gallium Arsenide (GaAs): Gallium arsenide is another substrate used, especially in high-efficiency solar cells. Gallium arsenide excels in soaking up sunlight due to its direct bandgap, making it a more effective choice than silicon for this purpose.
-
Cadmium Telluride (CdTe): This substrate is used in thin-film solar cells. CdTe cells have achieved efficiencies close to the Shockley-Queisser limit for single-junction cells.
-
Copper Indium Gallium Selenide (CIGS): Like CdTe, CIGS is used in thin-film solar technologies and is known for its high absorption coefficient and good efficiency.
-
Perovskites: Perovskite solar cells are a relatively new technology and have shown great potential in surpassing the Shockley-Queisser limit due to their tunable bandgaps and high absorption coefficients.
-
Organic Photovoltaics (OPV): These use organic compounds as the light-absorbing layer. While they don't match the power of inorganic counterparts, these materials win on flexibility and cost-effective manufacturing.
Exploring these materials, each with its unique strengths and hurdles, involves fine-tuning them to reach or even break through this benchmark of solar efficiency.
What is The Shockley-Queisser Limit?
In 1961 William Shockley and Hans-Joachim Queisser were the first scientist to calculate the maximum theoretical solar cell efficiency using a primitive single p-n junction. The theorectical limit was calculated to be around 33%. That means on a sunny day a silicon solar cell with one p-n junction could collect up to 33% of the sun's rays. Of course the technology was not there to come close to 33%, it was more like 10% for many reasons.
Today researchers are working hard to pass 20% effciency on cost-effective solar cells. Other materials and techniques are being researched to get us past 33% affordably.
Shockley–Queisser limit or detailed balance limit refers to the calculation of the maximum theoretical efficiency of a solar cell made from a single pn junction. It was first calculated by William Shockley and Hans Queisser:
William Shockley and Hans J. Queisser, "Detailed Balance Limit of Efficiency of p-n Junction Solar Cells", Journal of Applied Physics, Volume 32, pp. 510-519 (1961)
The Shockley–Queisser limit is calculated by examining the amount of electrical energy that is extracted per incident photon.
The calculation places maximum solar conversion efficiency around 33.7%assuming a single pn junction with a band gap of 1.4 eV (using an AM 1.5 solar spectrum). Therefore, an ideal solar cell with incident solar radiation will generate 337 Wm-2. When the solar radiation is modelled as 6000 K blackbody radiation the maximum efficiency occurs when the bandgap energy Eg=1.4 eV.
What Is The Shockley-Queisser Limit In Solar Cells?
The Shockley-Queisser limit is the voltage required for the open-circuit state of a solar cell. A solar  cell with a bandgap of 1.09 V will have an open-circuit voltage of zero. Its current density is governed by spectrum losses. Higher bandgaps absorb less photons, and the result is less current density. But, the Shockley-Queisser limit is a useful model for calculating open-circuit energy.
cell with a bandgap of 1.09 V will have an open-circuit voltage of zero. Its current density is governed by spectrum losses. Higher bandgaps absorb less photons, and the result is less current density. But, the Shockley-Queisser limit is a useful model for calculating open-circuit energy.
To get past this theoretical limit, solar cells must hit the Shockley-Queisser limit. This limits the maximum efficiency of the cell based on the conditions imposed by the silicon atoms in the cell. This limits the maximum output of the cell. The maximum conversion efficiency is 33.7%. The theoretical limit is the maximum amount of energy extracted per incident photon. The Shockley-Queisser limit is around 6000 K blackbody radiation.
The Shockley-Queisser limit can be defined as the theoretical upper limit of a solar cell based on the principle of detailed balance. It is the amount of electrical energy a solar cell can extract from an incident photon. Using the Shockley-Queisser limit, an ideal solar cell can reach up to 337 Wm-2 of output in a single exposure to incident sunlight.
A solar cell can't reach the Shockley-Queisser limit if it doesn't have any way to absorb photons. Its nominal power is the product of the open-circuit voltage Voc and the short-circuit current Ish. It's hard to achieve this with cell power alone, but impedance matching is possible. So, a multilayer solar cell can bump up the Shockley-Queisser limit.
While the Shockley-Queisser limit is often a good place to start developing a solar cell, it's important to note that the maximum solar cell efficiency is dependent on a few factors. Despite the Shockley-Queisser limit, multilayer cells require large amounts of light to be efficient. The cost of multilayer solar cells, on the other hand, is much lower. In addition, they are difficult to produce and use in a solar cell.
In solar cells, the Shockley-Queisser limit is the maximum theoretical efficiency of a solar cell. It has been calculated for decades by Hans Queisser and William Shockley, who published their paper in 1961. The Shockley-Queisser limit defines the upper limit for a single junction solar cell that uses an absorber material with a specific band gap. There are methods for surpassing the Shockley-Queisser limit, but they are not practical for solar cells.
The Shockley-Queisser limit is a theoretical upper limit for solar cells. The actual maximum solar cell efficiency varies with the temperature of the solar cell. For example, the maximum Shockley-Queisser limit for a single junction solar cell is 33.7%. By contrast, a single-junction solar cell with a band gap of 1.5 eV produces only 337 Wm-2 of electrical energy, which is significantly below the Shockley-Queisser limit for blackbody radiation of 6000 K.
The Shockley-Queisser limit is an upper theoretical limit for solar cells. It defines the maximum efficiency of a single-junction solar cell with a band gap of 1.4 eV. However, there are methods for solar cells to exceed the Shockley-Queisser limit without adding methods, and higher efficiencies are possible. This is the most important Shockley-Queisser limit.
The Shockley-Queisser limit is the maximum efficiency of solar cells based on the principle of detailed balance. It places the maximum solar conversion efficiency at 33.7% for a single-junction solar cell with a band gap of 1.4 eV and AM1.5 spectrum. The Shockley-Queisser limit can be exceeded without adding any additional methods. The Shockley-Queisser-Queisser-Queisser-limit is a critical threshold for commercial solar energy.
The Shockley-Queisser-limit is a theoretical limit for solar cells. It is used for semiconductors to generate electricity, as a result of solar radiation. The Shockley-Queisser-Limit is a limit of light-based devices. The most energy efficient ones are those with the lowest amount of spectrum loss. If there is an optimum, the Shockley-Queisser-Lower-Queisser-Limit value would be 1.2 eV.