I am researching the effects of intense radiation on different materials of varying ionization energies. Lately I have only been studying gases but would like to start studying semiconductor materials of varying band gaps. I am interested in getting some semiconductor materials but since I am just going to bombard them with radiation, I was wondering if you had an like scrap material from the dicing or like broken wafers. I dont want to spend over $100 per wafer its just going to get destroyed after about a minute of radiation. Can you let me know if you have any material such as this? I would be needing pieces about 1cm in length or larger of course, preferably the same in width, and thickness should not matter as I am studying surface defects for now.
It would also be ideal to have a variety of materials, Si, Ge, GaAs, InSb, InAs with some undoped, some doped n, some doped p.
Band Gap of Semiconductor Materials
Researching Iintense Radiation Effects on different Materials of Varying Ionization Energies
A nuclear engineering graduate student requested a quote for the following:
Reference # 213033 for specs and pricing.
Get Your Quote FAST! Or, Buy Online and and start researching today!
What is Band GaP?
Semiconductor band gap is the minimum amount of energy that is required to excite electron to free them from their bound state into a free state to conduct electricity. And is differnce between materials free state and its bound state and between the valence band and conduction band.
Below is a list of materials and their band gap. Let us know if you have any questions.
| Material | Band Gap eV |
|---|---|
| Silicon (Si) | 1.12 |
| Gallium Arsenide (GaAs) | 1.42 |
| Gallium Antimonide (GaSb) | 0.67 |
| Silicon Carbide (SiC) | 3.26 |
| Fused Silica | 9.0 |
| Single Crystal Quartz | 8.9 |
| Germanium (Ge) | 140 m |
How do you calculate the energy gap of a material?
The energy gap (also called the band gap) of a material refers to the energy difference between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). In a solid material, these are often referred to as the valence band and conduction band, respectively. The energy gap is a crucial property in semiconductors, insulators, and metals.
There are several methods to measure or calculate the energy gap of a material, depending on the type of material and the precise nature of the energy gap. These methods involve both experimental techniques and theoretical calculations:
-
Experimental Methods: Experimental methods are often used to determine the energy gap of a material.
-
Absorption Spectroscopy: The energy gap can often be determined from absorption spectroscopy, where the material absorbs light (or other electromagnetic radiation) and transitions from the valence band to the conduction band occur. By finding the point at which absorption begins to increase rapidly (the absorption edge), one can determine the band gap.
-
Photoluminescence Spectroscopy: In this method, a material is excited with a laser or other light source, and the emitted light is analyzed. The peak energy of the emitted light can be related to the energy gap of the material.
-
Electron Energy Loss Spectroscopy (EELS): This is a technique used in electron microscopes. A beam of electrons is sent through a thin sample, and the energy lost by the electrons due to interactions with the sample is measured. The energy loss can be used to determine the band gap.
-
-
Computational Methods: Theoretical methods can be used to calculate the energy gap. The computational approach involves solving the Schrödinger equation for the material's electrons, which is typically done using methods like density functional theory (DFT), GW approximation, or time-dependent DFT. These methods can give very accurate results, but they are computationally intensive and require significant expertise to carry out.
Keep in mind that all these methods have their strengths and weaknesses, and the most appropriate one will depend on the specific circumstances, including the type of material and the resources available. For complex materials or situations, multiple methods may be used in combination to get a more accurate determination of the energy gap.
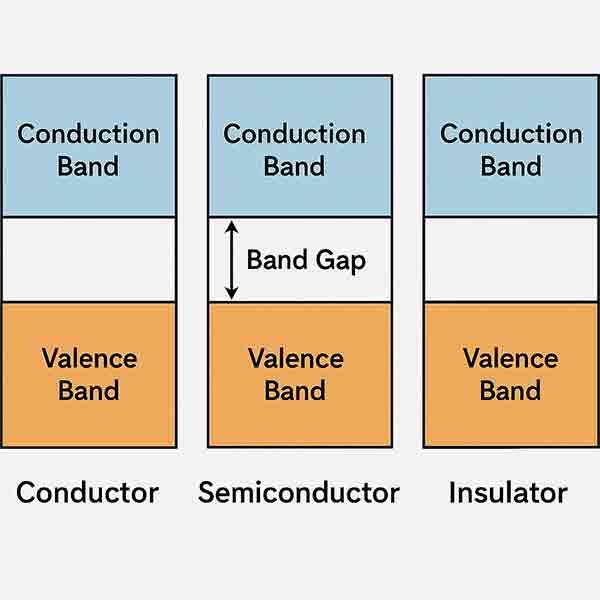
What Are the Effects of a Smaller Band Gap Than a Silicon Band Gap?
Having a narrower band gap in semiconductors makes them more conductive than other types. This is because thermal excitation creates a small population of the valence and conduction bands in a semiconductor. An applied electric field then rearranges this population to produce an electrical current. This effect is not consistent for all semiconductors. This is because the amount of energy required to promote electrons from a partially filled lower energy band to a completely empty, higher energy band is variable.
In regular semiconductors, the band gap is constant. This property is due to the presence of continuous energy states. However, in quantum dots, the band gap is size dependent. This effect is known as the quantum confinement effect and is a result of the fact that the semiconductor's size affects the band gaps. The larger the band gap, the less efficient the solar cell will be.
There are two ways to measure the bandgap energy of a material. First, you can calculate the bandgap of a material by using an electrical measurement method. Another way is to use spectroscopy. You can calculate the energy in a semiconductor by using an optical ellipsometry. The slope of the lnR vs. 1/T graph can be used to calculate the energy in a semiconductor.
Another way to determine the energy required for electrons to jump between two bands is by comparing the energy of the valence electrons of one material with the energy of its valence electrons in another. In addition to increasing the bandgap, you can also measure the atomic radius of germanium and silicon. The latter is a semiconductor with a large band gap, which is called a wide-band-gap semiconductor.
When it comes to the energy level, the bandgap energy is measured by the k vector. The k vector indicates the energy of the highest valence state. In contrast, the bandgap of the lowest valence state is the same. Therefore, these two measurements are not related. When these two variables are compared, the k vector will determine the energy in the valence and conduction band.
A smaller bandgap has many advantages over a silicon-based semiconductor. The bandgap is an important property of semiconductors that determines their ability to function under different conditions. Its larger bandgap is beneficial in applications that require fast switching and higher power, and it will also be more efficient in absorbing broad spectrum sunlight. It is essential to choose the right bandgap for semiconductors when the temperature is higher than 400 degrees.
When the temperature is higher than the bandgap, the valence electrons of silicon will be more energetic. Hence, the energy of the semiconductors decreases. As a result, the energy of photons is wasted as heat. Thus, the energy of the semiconductor is wasted. Besides, a smaller bandgap increases the energy of a solar cell.
While Si has a smaller bandgap than a silicon, GaAs and SiC semiconductors have a larger one. A narrower bandgap increases the temperature of a material. When the temperature is higher than the bandgap, the semiconductor is not conductive. A wider bandgap can prevent a malfunction. That means a device can function at a lower temperature.
When a material is in a solid state, it has a bandgap. In semiconductors, a smaller bandgap decreases its electrical conductivity. It is important to remember that a wider-bandgap means higher energy. So, it is best to avoid materials with a narrower-bandgap. It is necessary to consider all the possible side effects of the bandgap before deciding on a material.
What is Wurtzite Structures?
The wurtzite structures are named after the mineral wurtzite. They are a kind of 
crystal structure found in binary compounds. They are a hexagonal crystal system and are examples of hexagonal crystal systems. Their chemical prototype is ZnS. In this article, we'll discuss some of the interesting properties of these crystals. Listed below is a list of the different wurtzite structures.
The wurtzite structure is the most common crystalline structure of binary compounds. The hexagonal prisms in the corners are present in a wurtzite crystal. It is known to be a branch of the hexagonal crystal system. These crystalline structures are very common and are often found in nature. Some of the examples of wurtzite structure are shown below.
Another type of wurtzite structure is the cubic zincblende. This metal is composed of both zinc and sulfur. The ratio of the two atoms in the unit cell is 1:1. In addition, these materials have a cubic closet packing. The faces of these crystals are the same and the atoms are close together. This kind of wurtzite structure is similar to a face-centered cubic structure.
There are several different types of wurtzite structure. The closest structure is the hexagonal. The wurtzite crystals have hexagonal prisms in their corners. These structures are often found in zinc-blende. By annealing them to the right temperature, the two crystals can change to a wurtzite phase. Then the difference between these two phases is a matter of a few hundred million times larger than the difference between the zinc-blende and wurtzite.
The wurtzite structure occurs in a variety of compounds, including silver iodide, zinc oxide, and cadmium sulfide. It also occurs in gallium nitride, aluminium nitride, and zinc sulfide. The wurtzite structure is found in the hexagonal structures of many minerals, ranging from sulfur to silicon dioxide.
The wurtzite crystal structure is found in many compounds. It is made up of tetrahedral zinc and sulfur atoms. Its structure is hexagonal and resembles the ABABAABABAB pattern. In a wurtzite crystal, the yellow balls represent the metal atoms and the grey ones are the sulfur or selenium atoms.
The wurtzite structure is a type of hexagonal crystal system, and is similar to that of the zinc-blende. The two interpenetrating lattices are hexagonal and close-packed. The wurtzite structure has the same density as the zinc-blende. So, it's a great candidate for use in electronic components and displays.
There are many different wurtzite structures, and each has its own unique characteristics. The cubic zincblende structure is the most common type of wurtzite structures. Its hexagonal structure is very similar to that of cadmium sulfide. The wurtzite structure is the simplest form of this structure and is a branch of the hexagonal crystal system.
The wurtzite structures are a branch of the hexagonal crystal system. The structure is named for the mineral wurtzite. It is the most common crystalline structure of binary compounds, and it is a branch of the hexagonal crystal system found in many types of rock and soil. There are many other varieties of wurtzite, and the hexagonal structure is the most commonly found.
The wurtzite structure is a hexagonal structure composed of a single atom of zinc and sulfur. The wurtzite structure is the hexagonal crystal of zinc and sulfur. It is the only one of its kind to have a tetrahedral symmetry. It is a compound of zinc and sulfur. Wurtzite is a type of mineral found in many different countries.
Zinc blende and wurtzite are two forms of zinc sulfide. The former is hexagonal, while the latter is polymorphic. The two types are polymorphic. They are similar to zincblende, but they have different chemical compositions. Its hexagonal structure is cubic, while wurtzite is hexagonal. The ABABAB stacking of zincblende is called wurtzite.
Why Is Bandgap Important?
The bandgap is a critical factor in the working of light-emitting diodes and solar cells. It refers to the area of an atom in which electrons cannot participate in conduction. When an electron is excited, it can jump across the bandgap, which results in an electric current. There are several different types of band gaps and they can all have different functions. Using a simple MO picture, we can explain how bandgap affects energy levels.
The energy gap between the conduction band and valence bands determines the amount of energy required for an electron to break free. When an electron is free, it can take part in conduction. This energy gap is called the bandgap. It is often used to define the limits of conduction and optical devices. The narrower the bandgap, the higher the frequency. The widening of the bandgap helps improve device performance in power conversion and military applications.
When an electron breaks free of a lattice, it must have sufficient energy in the conduction band. The energy of the bandgap is the minimum energy required to excite an electron into the conduction mode. This energy is what causes excited electron-hole pairs to undergo recombination. This recombination produces photons with sufficient energy to participate in the process. A wide bandgap semiconductor is important for LED lighting.
In the case of semiconductors, a wide bandgap increases their operating temperatures. The wide bandgap makes it possible to operate devices at higher temperatures. They also have a higher critical electrical field density. This means that they can be used in more sophisticated and efficient power electronics. This has numerous benefits for a variety of industries, from the military to radio and power conversion. This opens up new opportunities for advanced technologies.
Typically, inorganic semiconductors have a small bandgap. The electronic bandgap is the area in which electrons have energy. For example, a semiconductor has a wide-bandgap because it is transparent and has a low-bandgap. This is because it has high-bandgap materials. And their properties allow them to function in higher temperatures than they would otherwise be possible.
A wider bandgap also allows devices to function at higher temperatures. These properties are beneficial in power-emitting devices. These devices can operate at higher power and higher voltages. In addition, they can operate at a greater temperature than conventional semiconductors. In contrast, semiconductors with a narrower bandgap can have problems switching larger voltages. This feature allows them to work at a much higher temperature than normal.
Wide-bandgap materials are more efficient in the electronics field. They can operate at higher temperatures than conventional semiconductors. The difference between the two bands is a major advantage for electrical devices. For example, a wide-bandgap material is more energy-efficient than a thin-bandgap material. However, the bandgap of a semiconductor is important because it can enable a device to operate at high temperatures.
A semiconductor can function at higher temperatures because it has a wider bandgap. The wider the bandgap, the more energy-efficient the material is. As a result, a wide-bandgap material has lower resistance. This is important for high-voltage devices and solar cells. In addition, a large-bandgap material can operate at higher temperature without generating excess heat.
The wide-bandgap material can operate at higher temperatures. It can withstand higher voltages and currents and is highly desirable for high-power applications. In addition, it can operate at higher temperatures. It is also valuable in power-conversion equipment. It can be useful in many different fields. It can also help in reducing energy costs. The broader bandgap material is a great benefit in many ways.
The bandgap is important in semiconductors. A narrow band gap increases the electrical conductivity of the material. It is the difference in energy levels between a semiconductor's valence band and conduction. In fact, the narrower the bandgap, the higher the energy of the semiconductor. This is one of the main reasons why a wide bandgap material is desirable. In contrast, a narrow-bandgap material can increase the size of the solar cell.
Can Material Having an Indirect Band Bap within Range 1.63eV-2.20eV for Photocatalytic Activity?
A material with an indirect band gap falls into two categories: an insulator and a semiconductor. The latter category is used for materials that are semiconducting or exhibiting a narrow bandgap. However, a large bandgap does not make a material a semiconductor. In this case, the energy levels of the two bands are identical. Moreover, the materials have a similar dimensionality.
The wavelength of a photon must be greater than the energy of the semiconductor's bandgap. Therefore, photovoltaic cells can only absorb light with a wavelength greater than the bandgap. If the bandgap is too small, the device would have a low operating voltage and very little energy per carrier delivered. Thus, the ideal material should have a large bandgap, enabling efficient absorption of broad spectrum sun light while providing high voltage output.
A material with an indirect band gap is one in which the valence band is dominated by radiation-induced effects. This means that the carrier in the conduction and valence bands is unable to find a hole with a suitable k vector. It must therefore undergo emission processes to complete the process. Some semiconductor materials with indirect band gaps are gallium phosphide, silicon, and germanium.
Indirect band gap semiconductor materials include gallium arsenide, indium gallium arsenide, aluminum nitride, zinc nitride, and lead sulfide. This is an important factor in the development of high-performance devices. If you want to know which material has the best optical properties, you must consider a number of factors.
Direct band-gap semiconductors are the best-performing types. This type of semiconductor is characterized by a large band-gap. For example, an electron in the conduction-band may annihilate a hole in the valence-band. This subsequently releases excess energy as a photon. The resulting light is a color-sensitive signal.
Indirect band-gap semiconductor materials have a narrow-bandgap. A material with a high indirect-gap semiconductor is characterized by a narrow-bandgap. The wavelength of the semiconductor is important. This enables the material to absorb light with the broadest bandgap. Indirect-gap semiconductors are commonly used in LEDs.
A material with a narrow-bandgap semiconductor is characterized by its low-voltage output. Its electrical conductivity is limited by the energy of electrons. It will only utilize the sunlight with long-wavelengths. Using a small-bandgap semiconductor will result in a low-voltage operation and poor utilization of short-wavelength photons. This means that a narrow-bandgap semiconductor must be selected for its wide-bandgap and high-voltage output.
Indirect-bandgap semiconductors have an increasing bandgap energy. The lower the bandgap, the higher the energy gap. Usually, the indirect-bandgap material has a higher bandgap value than the nitride semiconductor. Its high-bandgap transistors are less expensive, but they provide excellent performance.
Indirect-bandgap semiconductors are not suitable for light emitting diodes. This material's indirect-bandgap is a disadvantage, as it is less conductive than the direct-bandgap semiconductors. It is often necessary to enlarge the silicon layers in thin-film solar cells. A narrow-bandgap materials are more resistant to radiation, but are also more expensive.
Indirect-bandgap semiconductors are semiconductor materials whose bandgaps are not completely linear. The energy of a material's lowest energy state determines its band-gap value. Indirect-bandgap materials are referred to as 'narrow-band'. A narrow bandgap is useful for making infrared photodetectors and thermoelectrics.
An indirect-bandgap material is one with a large bandgap. Its electronic and optical bandgap are identical. The difference between these two is the Fermi energy. The higher the bandgap, the smaller the energy. The inversion of the spectrum will cause the material to lose a substantial amount of its electrons, which results in a higher-bandgap.
What is Bandgap in Semiconductor Materials?
The band gap in a semiconductor refers to the minimum energy needed to excite an electron so that it can participate in conduction. The band structure of a semiconductor illustrates two levels of energy: the lower energy level (called the valence layer) and the upper, or conduction, level. The band gaps between these two states are known as the transition states, and the difference between them determines the conductivity of a semiconductor.
The energy band gap is the difference in the energy level between the conduction and 
insulating bands in a solid. This difference is measured in electron volts, and is the same as the energy needed to liberate an outer shell electron. The free electron moves within the solid material, allowing it to perform electrical operations. The band gap is an important factor in determining the electrical conductivity of a substance. A large band-gap value indicates an insulator, while a small one indicates a semiconductor.
The energy difference between the two bands is known as the bandgap. In a semiconductor, this bandgap represents the minimum energy necessary to jump from one type to the other. The top of the valence band has the same electron momentum as the bottom of the conduction region, but the lower is the insulating layer, which is where the bandgap is the largest. This difference between the two bands is important for optical devices, like light-emitting diodes. Photons can produce an electron-hole pair.
The bandgap of a semiconductor is the difference between its valence and conduction bands. The smaller the bandgap, the greater the temperature difference. As a result, the bandgap of a semiconductor increases, making it more useful for high-temperature applications. In fact, a wide-bandgap material can operate even at 400 degrees Celsius. This difference in temperature enables it to work properly.
A semiconductor's band gap is determined by a combination of its electron and hole density. An electron has a higher density than a hole, so the more contrast between two elements, the higher the bandgap is. A high-energy semiconductor, on the other hand, is less dense. In a low-energy semiconductor, the bandgap is smaller. In this case, the electron has a higher mobility than its neighbor.
The bandgap is a difference between the energy levels of the electrons in a semiconductor. In a normal semiconductor, the band gap is the minimum energy difference between two adjacent electrons. In a quantum dot crystal, the bandgap is dependent on the size of the dot. A high-energy electron will be confined in its smaller size. Consequently, the quantum confinement effect is the cause of the large-energy difference between two particles.
The bandgap is the energy needed to excite an electron from one atom to another. There are three levels of energy in a semiconductor. The conduction band has the lowest energy. The valence band contains the highest energy. The valence band is where the electrons are confined. The conduction band has the lowest energy, so the light that passes through the semiconductor is blue.
A semiconductor's bandgap is a difference in energy between its valence and conduction bands. This energy difference is what allows electrons to jump across the bandgap. A low-energy bandgap will not allow an electron to move, while a higher-energy bandgap will allow an electron to move faster than one in the valence. So, the higher the valence, the greater the energy required to transfer an electric current from one state to the other.
The bandgap of a semiconductor is the difference between the valence and conduction bands. When an electron jumps from one of these two bands to the other, it enters the conduction band. This energy difference is the energy needed to move an electron from a valence to a conduction state. This gap is what allows an electronic device to communicate with other devices. When a person touches an LED, they are absorbing the light that hits the bandgap.
Is Band Gap the Same As Depletion Region?
The band gap is defined as the difference between electrons and holes in a semiconductor. The depletion region is a potential barrier across which electrons can't diffuse. The electric field in the depletion region is equivalent to the distance between the two regions. When the electron in the n-region tries to move to the p-region, it must climb this energy hill to achieve its destination.
The depletion region is a region of low-energy states of a semiconductor. This region contains a large number of electrons. In a semiconductor, a large portion of the electrons are in the conduction band. This makes the n-type region the depletion zone. In n-type semiconductors, the majority of electron carriers are in the n-type band.
In an indirect band-gap semiconductor, an electron that is excited by a photon of energy E g interacts with a lattice vibration called a phonon and gains energy. This process continues until the diffusion stops. It is only at this point that the depletion region is complete. If this is the case, an electron's energy is conserved, and it can't be used.
The Depletion Region Explained
A depletion region is a region where the majority of charge carriers are charged. In the n-type semiconductor, the carriers are free electrons, while the holes are charged. The charge diffusion between the n- and p-type semiconductors occurs because of the electric field opposing it. If the depletion region is the same as the depletion zone, then it would be a band gap.
In the depletion region of a semiconductor, the majority of charge carriers are charged. This means that the depletion region is a region of free electrons. In contrast, the depletion area has a large density of electrons. In the former, the electrons are surrounded by a weak electrical field. Both of these regions have different frequencies and will have different wavelengths.
The band gap is defined as the minimum energy change needed to excite an electron. The depletion region is characterized by the presence of both n-type and p-type electrons. For the n-type semiconductor, the electrons are a minority. In contrast, the p-type electrons are the majority. They are the semiconductors with high energy density. There are n-type semiconductors and p-type semiconductors.
The band gap in semiconductors is defined as the minimal change in energy needed to excite an electron. In the n-type semiconductor, this is the valence band. In n-type semiconductors, the electrons are in the trough of the conduction band. In such a case, they may move to the valence-band without involving phonons.
Generally, the band gap of a semiconductor is approximately 1.1 eV. When electrons are present in a depletion region, they will emit the same color as the opposite-type electrons. In contrast, a doped semiconductor will have a large spectrum of wavelengths. The bottom of the conduction band will have more holes than n-type. The dotted line represents the extra electrons in the conduction band. In the n-type semiconductor, the top of the n-type region is the same as the bottom of the p-region.
The depletion region is the overlapping region between the n- and p-type regions. This narrows the depletion region and reduces the barrier for carrier injection. The most important difference between the two is the energy level. The higher the energy level, the more ions can be neutralized. A thin depletion region increases the drift and diffusion components of the current. However, a thicker band gap can increase the diffusion and thermal energy.
When the band gap is narrow, electrons become confined in one or three dimensions. Unlike the latter, the electrons in a depleted region are indistinguishable from one another. A hole is created where the electron was formerly bound. This hole is not a part of the device but participates in conduction. This hole is known as an intrinsic semiconductor. This is where the band gap is.
The Mystery of the Bandgap
A semiconductor is a material with a narrower gap between the bands, allowing it to behave like both insulators and metals. Because of this, it has properties that lie somewhere in between. When semiconductors were first discovered, they were thought of as useless, but physicists solved the mystery of the bandgap, allowing people to harness these materials to make electronics and optoelectronic devices.
Direct bandgap
Inorganic semiconductors typically have small exciton binding energy and almost no electron-hole interaction, 
so the electronic and optical bandgap are identical. Most systems ignore this fact, but organic semiconductors and single-walled carbon nanotubes may have a large bandgap. To understand how this process works, consider the bandgap. It limits the energy of a single electron.
When electrons reach the band gap edge, they must move back to their original location. Typically, this requires an energy difference of several electron volts, or "band gap" energy. This energy is equivalent to the ionization and atomic potentials of the outer electron. The energy difference between the two bands is the minimum energy that the electron must pass through the band gap edge to return to its original position.
The k vector of a semiconductor is a critical factor in the process. It is important to note that the k vector of a material's bandgap affects the carrier's ability to find a hole. This reduction in recombination rate results from emission of a phonon. Some indirect band gap semiconductor materials are characterized by non-radiative recombination processes. Some examples include gallium phosphide, silicon, and germanium.
In general, this mechanism involves localized electrons wandering through the material. The result of this is that the radius of the band gap states are higher than the lattice parameters, so the recombination process is unsuitable. In this process, the number of electrons that are in the valence band does not decrease, so the energy is conserved.
Dielectrics
As the name implies, dielectrics don't allow current to flow through them. Instead, they are more often referred to as insulators, the opposite of conductors. Because of this, dielectrics are usually used to draw attention to their polarizability. This article will explain how dielectrics work and why they're important in electrochemistry.
A semiconductor's band gaps are the reason it can convert light into electricity. They can emit light as LEDs and make certain types of diodes. These processes rely on energy released or absorbed by electrons. However, dielectrics do absorb light, but not near infrared. These processes work because the energy released or absorbed by electrons causes a transition.
When electrons reach the band gap edge, they cannot fall below it, because of their lack of target states. Dielectrics are made up of two types of materials: semi-conductors and insulators. Electrons do not fall below the band gap edge in semiconductors because they can't fall below it, but they can do so if they get trapped between two different types of materials.
A dielectric-dependent version of PBE0 is known as PBE0DD. It is a self-consistent model of the band gap, which gives similar direct KS band gaps. The CTL method also assumes the presence of localized 3d states in some oxides. It is also called partial Mott-Hubbard.
Solids can either have a large or small band gap, which determines their electrical conductivity. Semimetals with a large band gap will conduct electricity, while those with a narrow band gap will not. This is why they're called semiconductors. Dielectrics can be made to be both conductive and non-conductive depending on the conditions.
Extrinsic semiconductors
If an electron reaches the edge of a band structure, it must change its quantum state to fall into the other band. The band structure gives a map of the only states allowed in a material. When an electron reaches the edge of the band structure, it must jump to another band, because the energy of a photon causes an "excitation" of the electron.
The band structure is similar to a map of all the different quantum states in a material, where the electrons have energy levels that correspond to their angular momentum. The properties of a material depend on the energy level that is closest to the Fermi energy, and materials with such a band structure are good conductors of electricity, light, and magnetic things. Researchers use various methods to study band structures, including X-ray measurements and laser beams.
When an electron reaches the edge of a band, it must find a hole in the valence-band in order to fall into the conduction band. This is a process known as electron-hole pair generation. Thermal energy is constantly emitted in this process, and the electron-hole pair is likely to recombine with the same hole. Ultimately, if an electron does not fall below the edge of the band, the energy it has to move to the valence band will be emitted.
If the band-gap energy is equal to the amount of energy in the conduction band, the electrical potential between the two contacts is maximal. In semiconductors with smaller band gaps, this is also true. In semiconductor materials with a small band gap, the energy levels in the valence band will be smaller than in the conduction band. And thermalization also happens in the valence band. When electrons are excited to the conduction band, they leave holes in the valence band. Electrons from higher up fill these holes, especially near the band gap edge.
Graphene
The structure of graphene nanoribbons is very similar to that of DNA. When a graphene electron reaches the band gap edge, it doesn't fall below it, but they may remain above it for a few atoms. This effect is called Anderson localization. Graphene electrons don't fall below the band gap after they reach the edge of the band gap, because they do not fall below it once they've reached the edge.
The large energy band gap in graphene was engineered by the researchers. The graphene layer was grown on a silicon carbide substrate to produce a large energy band gap. The researchers measured the band gap, calculated the expected outcomes, and tested their theories against experiment. The results were in agreement with their theoretical predictions. They were able to prove the effectiveness of the technique.
The researchers at MIT discovered that graphene electrons don't fall below the surface of the band-gap edge, despite the fact that they have no free space at the edges of the graphene sheet. Moreover, they found that the edge mode movement of graphene electrons was counter-propagating. These results provide a deeper understanding of how graphene works.
The difference between the in-plane and out-of-plane distortions in penta-graphene has been shown to be a factor of three. It appears that penta-graphene experiences the largest distortions because it has an oxygen atom at the A site. Moreover, the difference between the in-plane and out-of-plane dipole moments is approximately the same.
Silicon
Many scientists have been puzzled by the observation that electrons in bulk silicon do not fall below the band-gap edge. This could be due to a number of different processes and optical transitions. Some of these processes are unknown, however. In this article we will discuss two theories. The first hypothesis assumes that electrons drift through bulk silicon and form a covalent bond with atoms that are further apart. The second theory assumes that the added atoms make for more bonds.
Another possibility is that the ion implantation process induces a higher number of mid-bandgap energy levels in the silicon crystal. Increasing the bias voltage makes the Schottky barrier closer to the silicon/metal interface. This shift increases the efficiency of the barrier collection. Another possibility is that the electrons "bump" into the Si atoms and transfer their excess energy to them. Eventually, this process is called thermalization, where the electrons relax at the conduction band edge before contact. The heat generated causes a large amount of energy to be lost.
The third explanation is that the silicon-germanium alloy crystals are hexagonal and have an irregular structure. This structure differs from diamond. The alloy produces nanowires that emit infrared light, and the device is useful for optical communications and computing. Eventually, this silicon-based alloy may be used to create chemical sensors. Therefore, this theory will allow for new breakthroughs in silicon photonics.
The next theory is that silicon is made of a type of silicon that enables electrons to fall beneath the band gap edge. In pure silicon, there are four types of silicon atoms - P-type silicon, N-type silicon, and C-type. P-type silicon is the most common type of semiconductor material, and it has the lowest band-gap edge, a phenomenon known as the 'band gap'.